関数 2乗に比例する関数とは 2乗に比例する関数のグラフ 2乗に比例する関数 変域・変化の割合;相似 相似 線分比・相似の定理 相似と面積比・体積比; 二次関数も、一次関数を解くのと同じ感覚で解いていけばいいのです。 二次関数は、例えば「 y=ax2 」と表記します。 a に「 2 」を入れれば「 y=2x2 」になります。 これは、「 y は x の二乗の 2 倍」にすぎません。 先ほどの「 y=2x 」の「 x 」が「 x の二乗」に変わっただけです。 二乗は「同じ数を掛ける」だけなので、難しくありません。 「 y は x の二乗の 2 倍
関数 図形の解き方 商品情報 好学出版
関数の解き方
関数の解き方-<キーワードを見つければ ⇒ 決まった解き方が! > 1 「1次関数」「直線」 とあったら、 ⇒ はじめに 「y=ax+b」 と書く。 2 「変化の割合が」「傾きが」 とあったら、 ⇒ 「a」 に数値を代入 「切片が」 とあったら、 ⇒ 「b」 に数値を代入 3 この問題が分からなくて困ってます。解き方を教えてください! 高校 教えて!goo




中学数学 二次方程式の解き方はこの3パターンだけでok 平方根 因数分解 解の公式 楽スタ
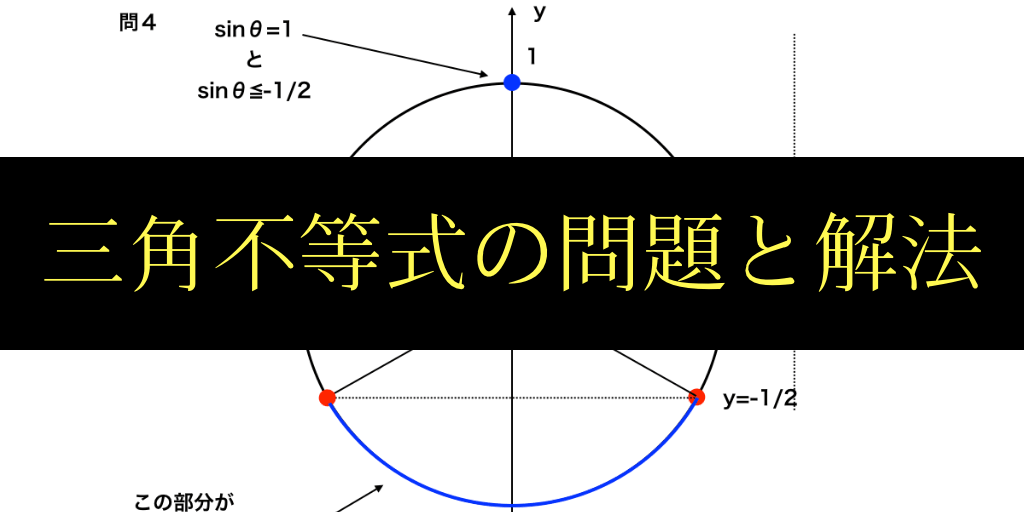
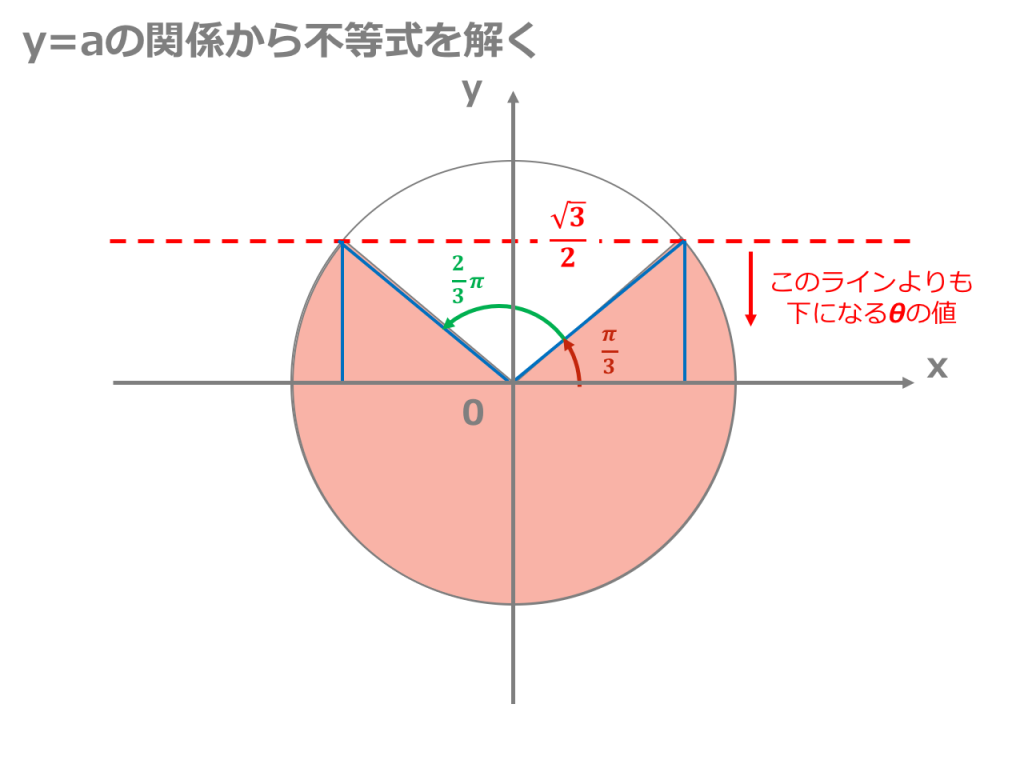
三角関数sinθを含む不等式の解き方①:sinθ=aを満たす角度を求める 不等式を解く上で最初にやることは、不等式を「sinθ=a」と置き換えた上でそれを満たす角度を求めることです。 sinθはy座標に対応するので単位円上でy=aと交わる点を求めると以下のようになります。 この図より30°、60°、90°の三角形が出来上がっていることがわかるので、 を満たすθは となり まず、問題にある関数を理解するところから始めてください。 f (n,k)という関数は、次の三つの条件で計算方法がかわります。 「k=0」のときは、「f (n,k)=1」になります。 「0問題の解き方のコツと勉強法! 難問にも対応 高校数学の二次関数とは何? わかりやすく解説 高校数学で取り扱われる「二次関数」。 「センター試験の過去問が、最初の数問で詰まってしまう」 「課題で出された問題集が、解説を見ても分からない
関数方程式の解き方のコツ〜全射と単射〜 全射と単射: 行き先の候補となるどんな元 y y y を持ってきても f ( x ) = y f(x)=y f ( x ) = y となる x x x が存在するとき, f ( x ) f(x) f ( x ) は全射である と言う。 このとき、f(2) = 2 × 22 a × 2 a2が最大値です。 こんな感じです。 ここまでをまとめると、こんな感じですね。 最小値は、 f(2) = 2 × 22 a × 2 a2 ( {\frac {a} {4} > 2} のとき) f(a 4) = 7 8a2 ({0 二次関数の問題です。 解き方と答えを教えて下さい。 問題 右の図のように、関数y=2x²,関数y=½x²のグラフ上に、4点a,b,c,dをとり、四角形acdbが正方形となるようにとる。ただし、abはx 軸に平行である。このとき、正方形acdbの面積を求めよ。
f (f (x)) = f (x) 2 f (0) f(f(x))=f(x)2f(0) f (f (x)) = f (x) 2 f (0) という関数方程式において, f (x) f(x) f (x) が全射なら, f (a) = 0 f(a)=0 f (a) = 0 となる a a a が存在するので,もとの関数方程式に x = a x=a x = a を代入すると f (0) = 2 f (0) f(0)=2f(0) f (0) = 2 f (0) より f (0) = 0 f(0)=0 f (0) = 0 が分かる。三角関数の解き方|高校生/数学 数学は僕に任せてください! いきなりですが、下の問題見てください。 aは定数とする。 θに関する方程式cos2θsinθa=0について、次の問いに答えなさい。 ただし、0≦θ<2πとする。 (1)この方程式が解をもつためのaの条件を求めよ。 (2)この方程式の解の個数をaの値の範囲によって調べよ。 この問題を初見で解くことが数学B ベクトルの問題をすらすら解けるようになる方法 加藤 こんにちは。 加藤です。 今回はベクトルの「解き方」について解説していきます。 ベクトルって「解説を読めばなんとなく理解はできるが、いざ自力で解こうとしても方針が全く




2次方程式 1 解き方 因数分解 平方根 平方完成 解の公式 バカでもわかる 中学数学



1
一次関数の問題の解き方 パターン1~3文章から一次関数の式を求める パターン4グラフから一次関数の式を求める パターン5与えられた一次関数の式をグラフに書く パターン6\(x\)の変域から\(y\)の変域を求める そもそも三角方程式と 最も基本的な「置き換え」を利用するタイプから始めましょう。 sin2θ 2sinθ1=0 (0≦θ<2π ) この程度であれば置きかえずに因数分解して解けるかと思いますが、 一応:sinθ=t と置いてといていきます。 三角方程式の解き方について学習するページです。 三角方程式の基本的な解き方と一般解を利用した解き方について問題演習を通して学習だけど、 関数って入試にめっちゃ出るじゃん(泣) という方のために、 高校入試によく出題される関数のパターン、ポイントをまとめていきます。 関数の勉強、何やったらいいか分からんって人は参考にしてくださいね (/・ω・)/
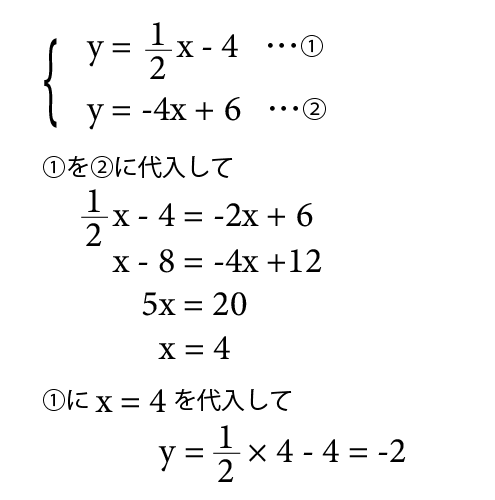



中学2年生数学 1次関数 グラフと図形 長野地区 Itto個別指導学院 長野市の学習塾




ゆっくり実況 一次関数 点pの式 解き方 中2 数学 Youtube
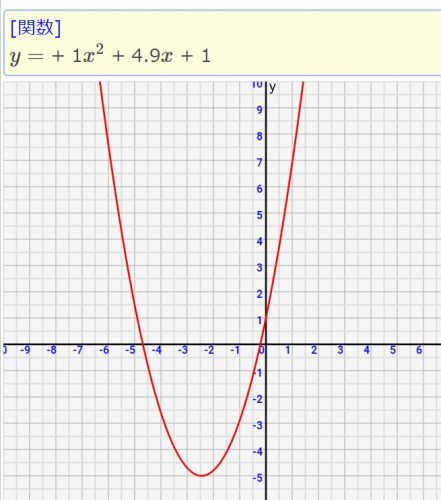
よーくみると、 関数に「入れるもの」と「出てくるもの」は変化しているね? ? AをいれたらBがでてくるし、CをいれたらDが出てくるっていう感じで。 だから、数学では、 この「入れるもの」と「出てくるもの」を「 変数(へんすう) 」って呼んでいるんだ。 そんで、中学校で勉強する関数はほとんど、っていうか、たぶん全部が、 Aを「x」、Bを「y」として ax^3bx^2cxd = a (x \alpha) (x \beta) (x \gamma) \ \cdots ① ① が成り立つ。 ①の両辺を a \ (a \neq 0) で割ると \displaystyle x^3 \frac {b} {a}x^2 \frac {c} {a}x \frac {d} {a} = (x \alpha) (x \beta) (x \gamma) \ \cdots ② ② ②の右辺を展開して整理すると ③の両辺の係数を比Y = − 3 x 2 y = x 2 y = 1 2 x 2 このように、式によって x 2 の前にある数字が変わります。 そのため二次関数は以下の公式によって表されます。 y = a x 2 二次関数で最も基本的な式が y = a x 2 で表される方程式です。 リョースケ大学 一次関数の解き方:傾き・切片でのグラフの書き方、交点の求め方




連立方程式で3つの式がある時の解き方が誰でも分かる 高校生向け受験応援メディア 受験のミカタ




二次関数の利用の問題の解き方 グラフ無 はやさ 1 現役塾講師のわかりやすい中学数学の解き方
関数のグラフとx軸に囲まれた面積の求め方 2つの関数のグラフに囲まれた面積の求め方 実数解を持つ高次方程式の解き方 (方程式機能/グラフ機能/ソルブ機能)関数電卓では、画面の上部に入力した数字や記号が表示されます。 入力方法は通常の電卓と同じく、該当するハードキーを押下することで入力します。 例 12+38 足し算記号は のキーを入力します。 入力が完了したら、 を押下します。 操作方法 分数関数とは? グラフや微分・積分、不等式の解き方 21年2月19日 この記事では、「分数関数」についてわかりやすく解説していきます。 グラフの書き方や不等式の解き方、微分・積分の計算なども説明しますので、この記事を通してぜひマスターして




方程式 小数点があるときの計算 解き方を解説 Youtube




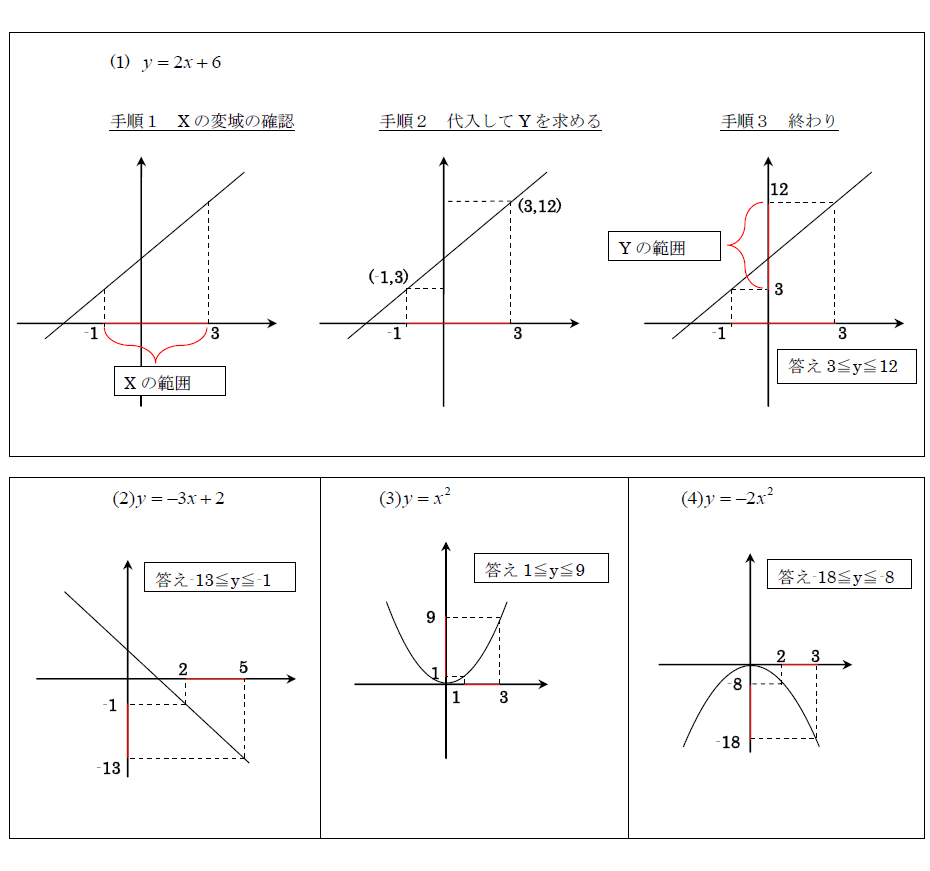
一次関数 変域問題の解き方 変域から式を求める方法とは 数スタ
三角関数の不等式の解き方 三角方程式の基本形( sinθ≧c sin θ ≧ c , cosθ≧c cos θ ≧ c , tanθ≧ c tan θ ≧ c , 不等号は≧,≦,>,<のいずれでもよい ) に式を変形して解く. sin(aθ−b) ≧c sin ( a θ − b) ≧ c , cos(aθ−b) ≧ c cos ( a θ − b) ≧ c , tan 二次関数の平行移動の解き方:公式はなぜマイナス? 投稿日:年11月30日 更新日:年12月1日 こにちは、今日は高校数学I、二次関数の平行移動のやり方について見てみましょう! 平行移動の公式、プラスとマイナスが混じって混乱しやすいですね 二次関数の対称移動の解き方:軸や点でどうする? 公式や因数分解の解き方の簡単な方法を問題を解きながらマスターしていこう! 目次1 因数分解の解き方1:共通因数をくくりだす 大学入試:英語の民間試験活用予定公表、問題点は?




中学1年数学 一次方程式 一次方程式の解き方 移項の本当の意味を理解すれば全部解ける 数学の面白いこと 役に立つことをまとめたサイト



関数 図形の解き方 商品情報 好学出版
他の三角関数についての難しい微分計算は >sin,cos,tanの微分例題を解説!2乗、分数のときにはどうやる? こちらの記事でまとめているのでご参考ください。 指数、対数関数の導関数 一次 関数 問題 解き方 一次関数の問題の解き方7パターン 管理人 2月 16 19 一次関数はいろいろな問題が出されるので混乱してしまうかもしれませんがパターン自体は決まっているので慣れてしまえば簡単に解けるようになります2次方程式 2次方程式の解き方 2次方程式の応用 文章題;



二 次 関数 数学入門 二次関数をシミュレーション 図解で理解 Amp Petmd Com



三次関数とは グラフや解き方 接線 極値の求め方 微分 受験辞典
三角関数を含む積分の基本 ここでは、まず積分で使う三角関数の公式を確認します。 主に数Ⅱの三角関数にて習ったものがほとんどです。 積和の公式については、発展的な公式なので、学校によって習うかどうか差があるかもしれませんが、数Ⅲを勉強する人は使えるようにしてほしい公式です。 その公式を今回は、しっかりと確認しておきましょう。 ここで こんにちは。 da Vinch (@mathsouko_vinch)です。 指数方程式が解ければ対数方程式も解ける?対数の計算をやったら指数と同じようにやはり方程式と不等式を解けるようにならねばなりません。ですが安心してください。指数の計 y = ax^b cx^d eという指数関数の方程式を仮定した場合、定数a,b,c,d,eを求めることは可能でしょうか?素人考えだと、未知の定数が5つあるため、5つの連立方程式を使えば算出できそうな気がするのですが、代入法と加減法で一つずつ定




平成25年長野県立高校 入試問題 二次関数の変域の問題の解き方 現役塾講師のわかりやすい中学数学の解き方




中学数学 1次方程式 文章題の解き方 速さ 時間 道のり
①関数を微分して,導関数を求めよう。 ・公式 ②導関数の値が 0 になるときをヒントに,符号の変化を考えよう。 ③増減表を作り,極値を求めよう。 ・極値をとるとき (導関数)=0 であっても,



一次関数の利用を解説 グラフの書き方や解き方を知り入試に活かそう Studyplus スタディプラス




二次関数のグラフと問題の解き方 覚えておくべき2つの公式



Studydoctor微分方程式の解き方 高校数学 Studydoctor




二次関数の解き方 Tonoma1981 Note



三角関数を含む不等式の解き方と単位円を使うコツ




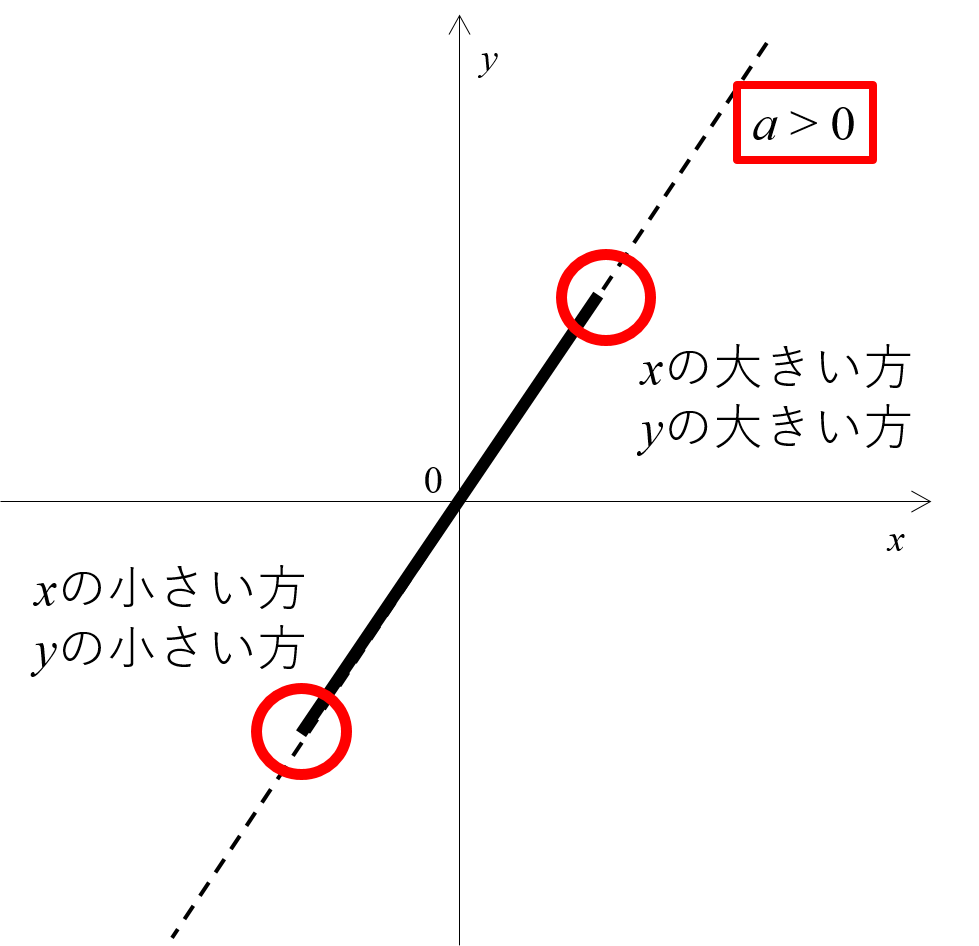
Mathematics 1次関数 6 応用問題の解き方 1 1次関数と図形 働きアリ
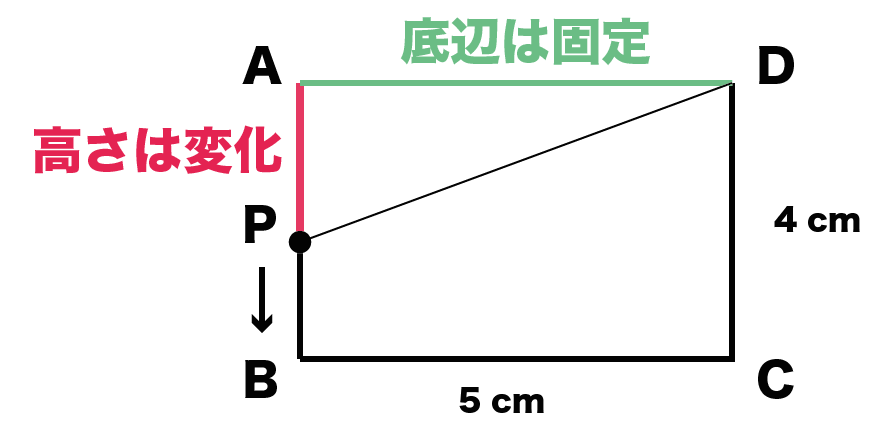



一次関数の利用 動点の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
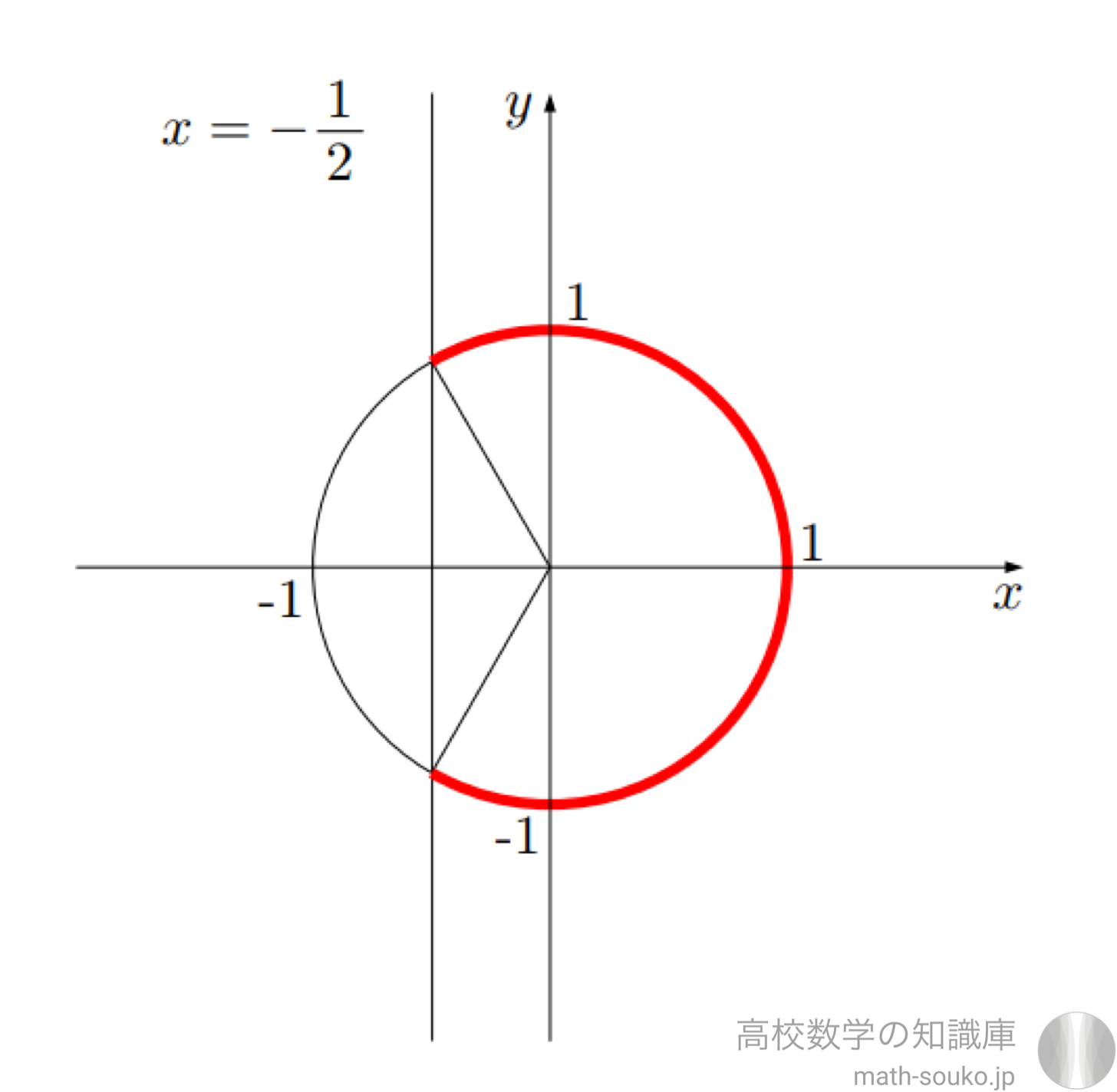



三角関数のはいった方程式 不等式の見極め方と解き方 その2 弧度法 高校数学の知識庫



中3数学 いろいろな関数の問題の解き方がわかる4ステップ Qikeru 学びを楽しくわかりやすく




一次関数の基本問題の解き方 2直線 現役塾講師のわかりやすい中学数学の解き方




Xyz 3つの式の連立方程式の解き方がわかる4ステップ Qikeru 学びを楽しくわかりやすく



1次関数 2次関数の変域 中学数学 受験 定期試験 数学解き方集 裏技 解法




中学数学xやyの意味と使い方がわかる わかりにくいxやyの意味と 問題の解き方がわかる 方程式 関数 因数分解 式の計算の通販 小林道正 紙の本 Honto本の通販ストア




一次関数の利用の問題の解き方 グラフ 1 現役塾講師のわかりやすい中学数学の解き方




一次関数の解き方 傾き 切片でのグラフの書き方 交点の求め方 リョースケ大学




連立方程式 A B C の形をした方程式の解き方をイチから解説 Youtube




3次方程式まとめ 解き方 因数分解 解と係数の関係 理系ラボ




高校数学2次関数 の解き方を教えてください Clear




完全版 一次関数のグラフから利用問題まで解き方まとめ 中学数学 理科の学習まとめサイト



2



三次関数とは グラフや解き方 接線 極値の求め方 微分 受験辞典




数学 一次関数の定義域 値域とは 問題の解き方を解説 数スタ




二次関数のグラフと問題の解き方 覚えておくべき2つの公式




中1 数学 中1 30 方程式を解く 小数と分数編 Youtube




中学数学 二次方程式の解き方はこの3パターンだけでok 平方根 因数分解 解の公式 楽スタ



1次関数 変域を使った問題の解き方2 数学がわかるブログ
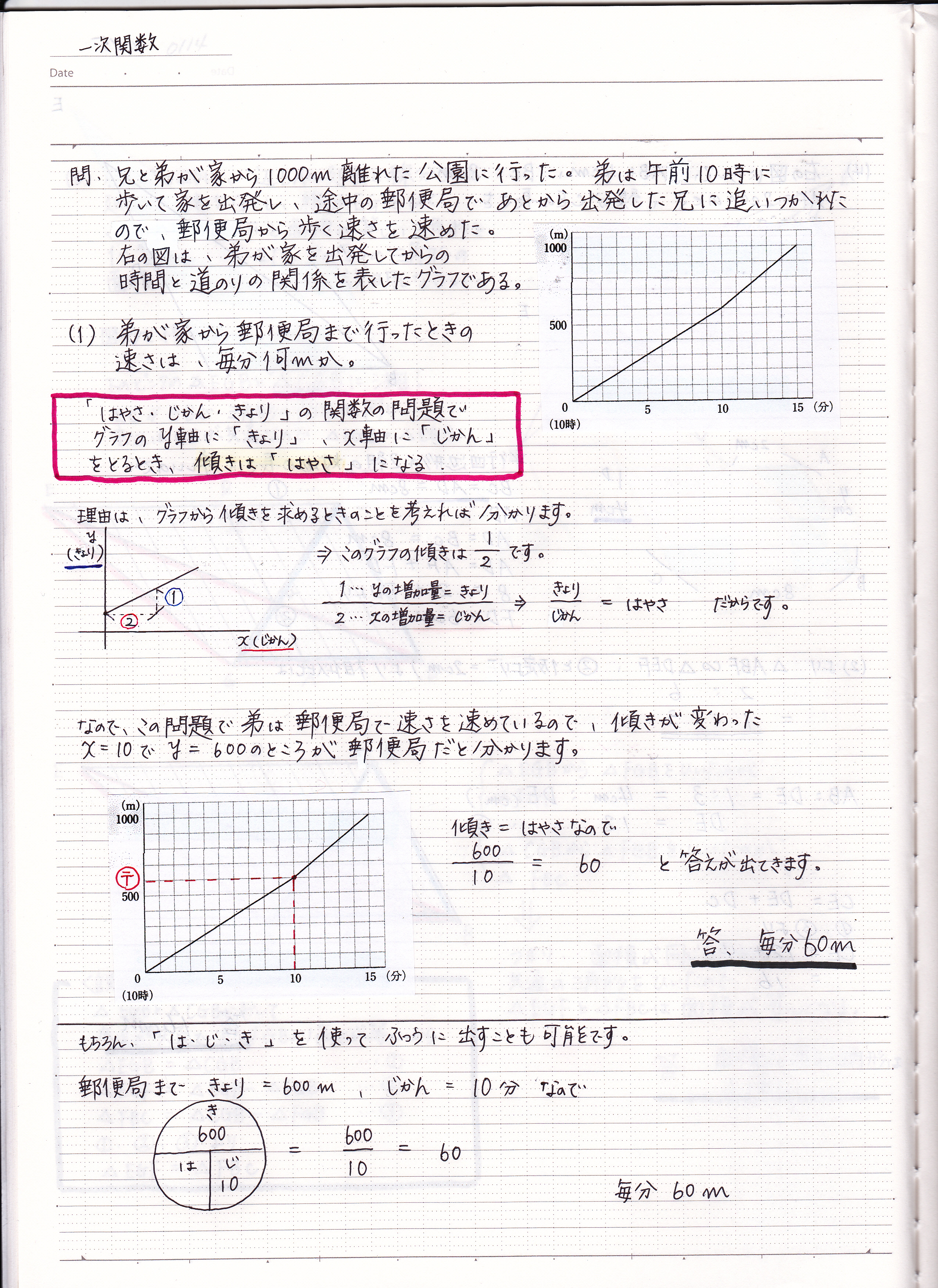



一次関数の利用の問題の解き方 速さ 2 現役塾講師のわかりやすい中学数学の解き方
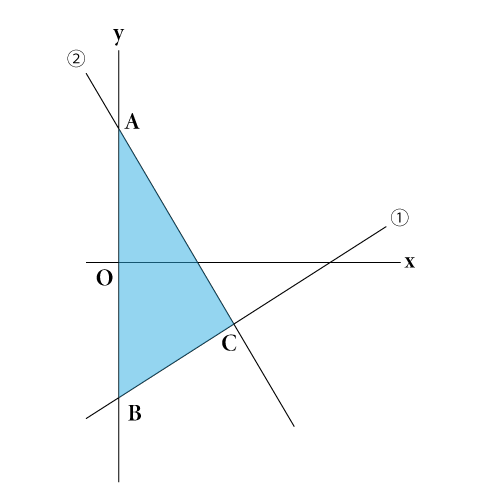



中学2年生数学 1次関数 グラフと図形 長野地区 Itto個別指導学院 長野市の学習塾
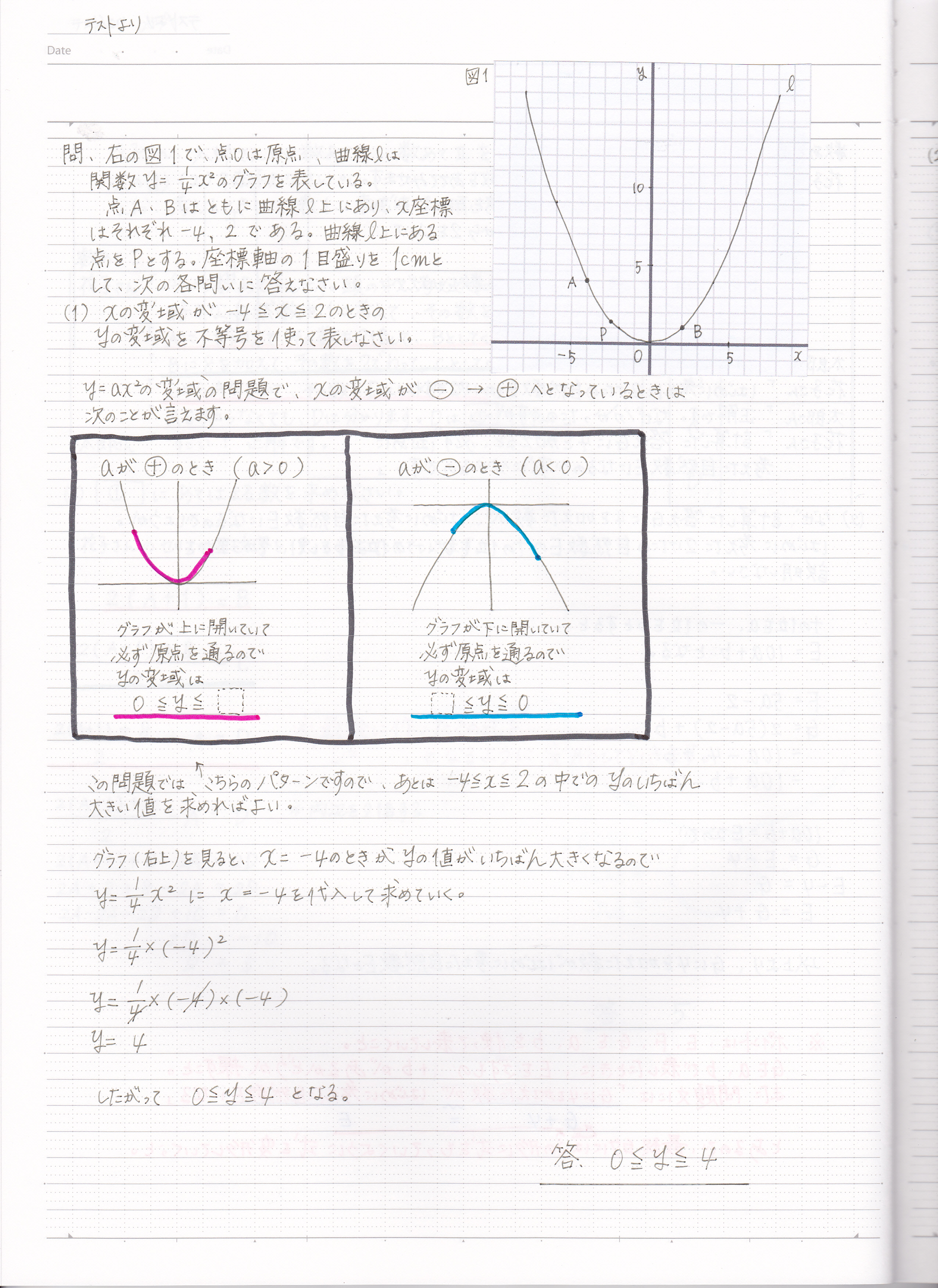



二次関数と一次関数の融合問題の解き方 変化の割合 座標 式の求め方など 現役塾講師のわかりやすい中学数学の解き方



Q Tbn And9gctk9fjul0shqxzmjnpxysfi Agrkj7cyp Qn 8fd5znx4r67rtn Usqp Cau




この二つの関数の問題の解き方を教えて下さい Clear




連立方程式の解き方とは 代入法か加減法で計算しよう 分数の問題や文章題アリ 遊ぶ数学




指数関数の解き方 写真の問題の最後の解き方が分かりません なぜあ 数学 教えて Goo



一次関数のグラフを書く問題で Yについて解く 解き方と それぞ Yahoo 知恵袋




二次方程式の解き方 平方根の知識を使う問題のパターン 中学や高校の数学の計算問題




高校数学 2次不等式の解き方1 X A X B 0など 練習編 映像授業のtry It トライイット
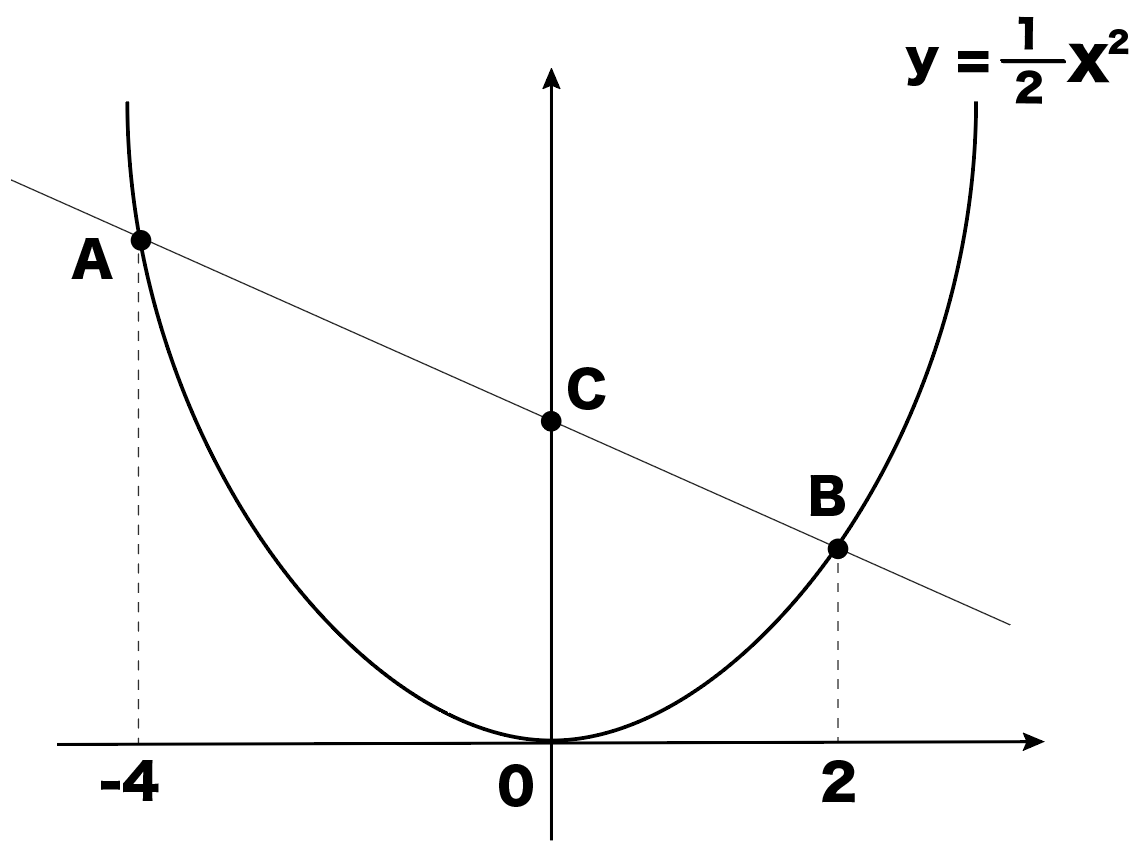



二次関数のグラフで三角形の面積を求める問題の解き方4ステップ Qikeru 学びを楽しくわかりやすく



一次関数とは グラフの書き方や一次関数の利用問題の解き方 受験辞典




一次関数の利用の問題の解き方 速さ 3 現役塾講師のわかりやすい中学数学の解き方




数学関数のコツ 入試必出の関数問題の解き方がわかる 秀英books 今春幸久 本 通販 Amazon



3分でわかる 三角関数の不等式の解き方 合格サプリ



一次関数とは グラフの書き方や一次関数の利用問題の解き方 受験辞典




中学数学の二次関数 問題の解き方の基本とグラフの書き方 リョースケ大学
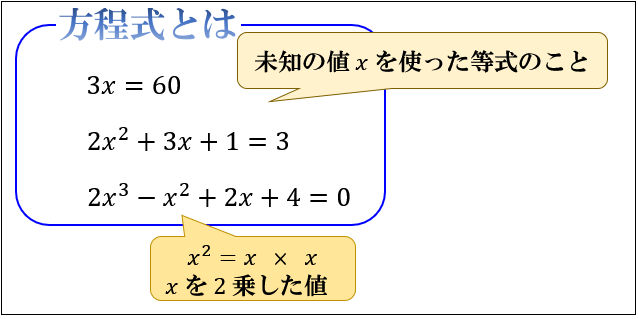



二次方程式の意味と解き方まとめ 解の公式 因数分解 アタリマエ




一次関数の利用の問題の解き方 速さ 1 2 現役塾講師のわかりやすい中学数学の解き方
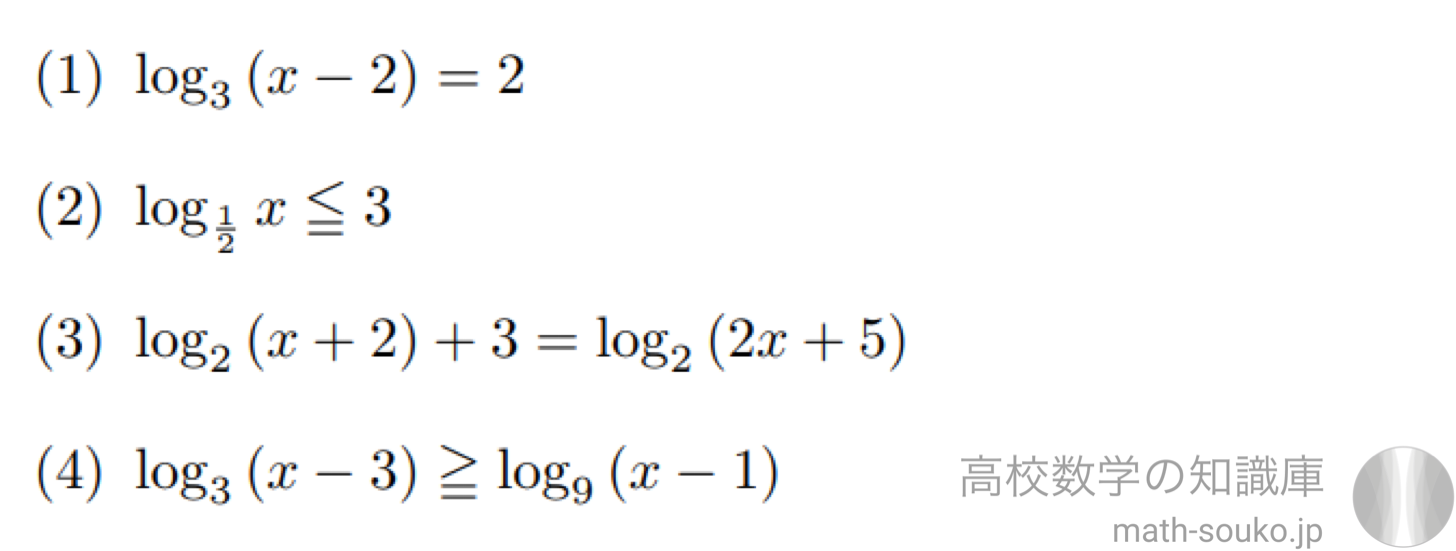



対数方程式と対数不等式の解き方 高校数学の知識庫




中学数学関数とグラフ問題の解き方 旺文社 本 通販 Amazon



この二次関数の問題の解き方とグラフの答えを教えて欲しいです Yahoo 知恵袋



1




一次関数の問題の解き方 7パターン 数学fun




一次関数とy Ax2乗の変域の解き方を分かりやすく教えてください 例題なんで Clear



48s96ub7b0z5f Net Taisuu Houteishiki




ヤフオク 関数とグラフ問題の解き方 中学数学 2色刷 寺田




3次方程式まとめ 解き方 因数分解 解と係数の関係 理系ラボ




連立方程式の利用の問題の解き方 年齢の問題 1 現役塾講師のわかりやすい中学数学の解き方




高校数学で学習する連立方程式の解き方まとめ 数スタ




高校数学で学習する連立方程式の解き方まとめ 数スタ



一次関数の利用の問題の解き方 グラフ 3 現役塾講師のわかりやすい中学数学の解き方



1



中3 二次方程式の解き方 解の公式 中学数学の方程式 中間 期末テスト 高校入試対策




数学 中2 32 一次関数の式をもとめる 基本編 Youtube




受験 定期試験 数学解き方集 裏技 解法 2次関数 高校




中1方程式 分数が含まれるときの解き方を問題解説 Youtube




この二つの関数の問題の解き方を教えて下さい Clear




中2 受験生 一次関数 できる人の関数グラフの解き方 デジタル板書データ Youtube
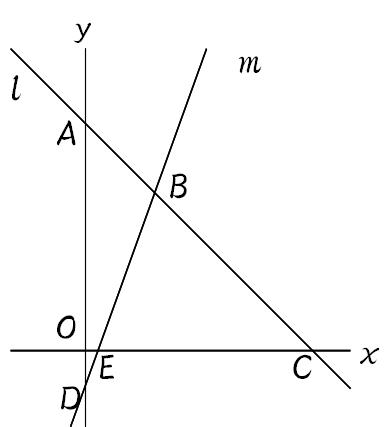



Mathematics 1次関数 6 応用問題の解き方 1 1次関数と図形 働きアリ




数学関数のコツ 入試必出の関数問題の解き方がわかる 秀英books 今春幸久 本 通販 Amazon



しょうちゃん 公式ブログ 2次方程式の新しい解き方を解説 Powered By Line




連立方程式の利用の問題の解き方 平均の問題 1 現役塾講師のわかりやすい中学数学の解き方




数 二次関数と二次不等式の解き方の違いとは 高校数学をわかりやすく解説 Youtube




中2 一次関数です 解き方と理屈を教えて欲しいです Clear



中3数学 いろいろな関数の問題の解き方がわかる4ステップ Qikeru 学びを楽しくわかりやすく



二次関数のグラフの書き方と公式を使った最大値最小値問題の解き方 Studyplus スタディプラス
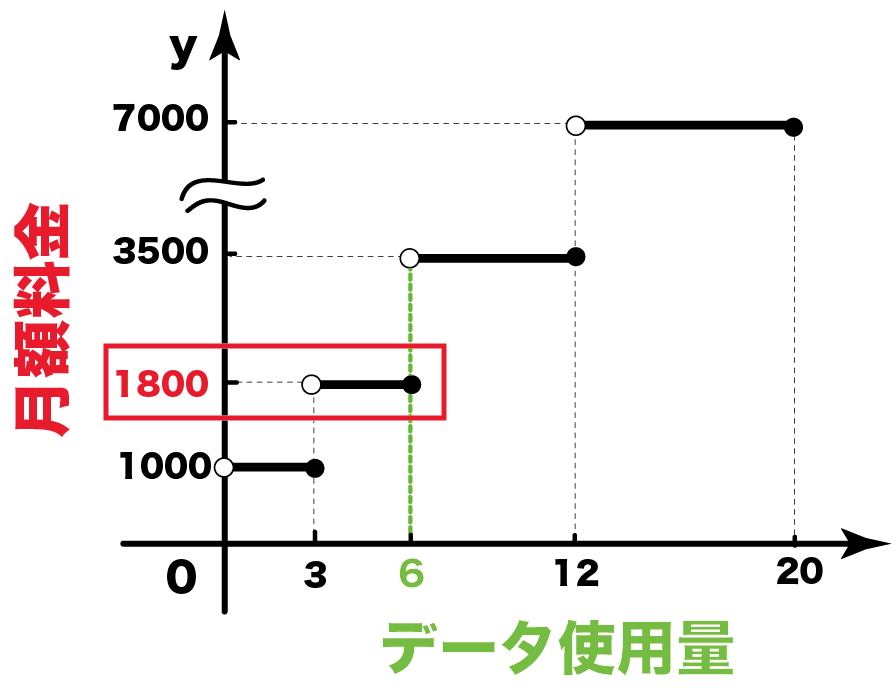



中3数学 いろいろな関数の問題の解き方がわかる4ステップ Qikeru 学びを楽しくわかりやすく




数学 二次関数が簡単になる解き方とグラフの書き方 札幌市 学習塾 受験 チーム個別指導塾 大成会




二次方程式の解き方のまとめ 中学生に覚えてほしいパターンは5つ 中学や高校の数学の計算問題
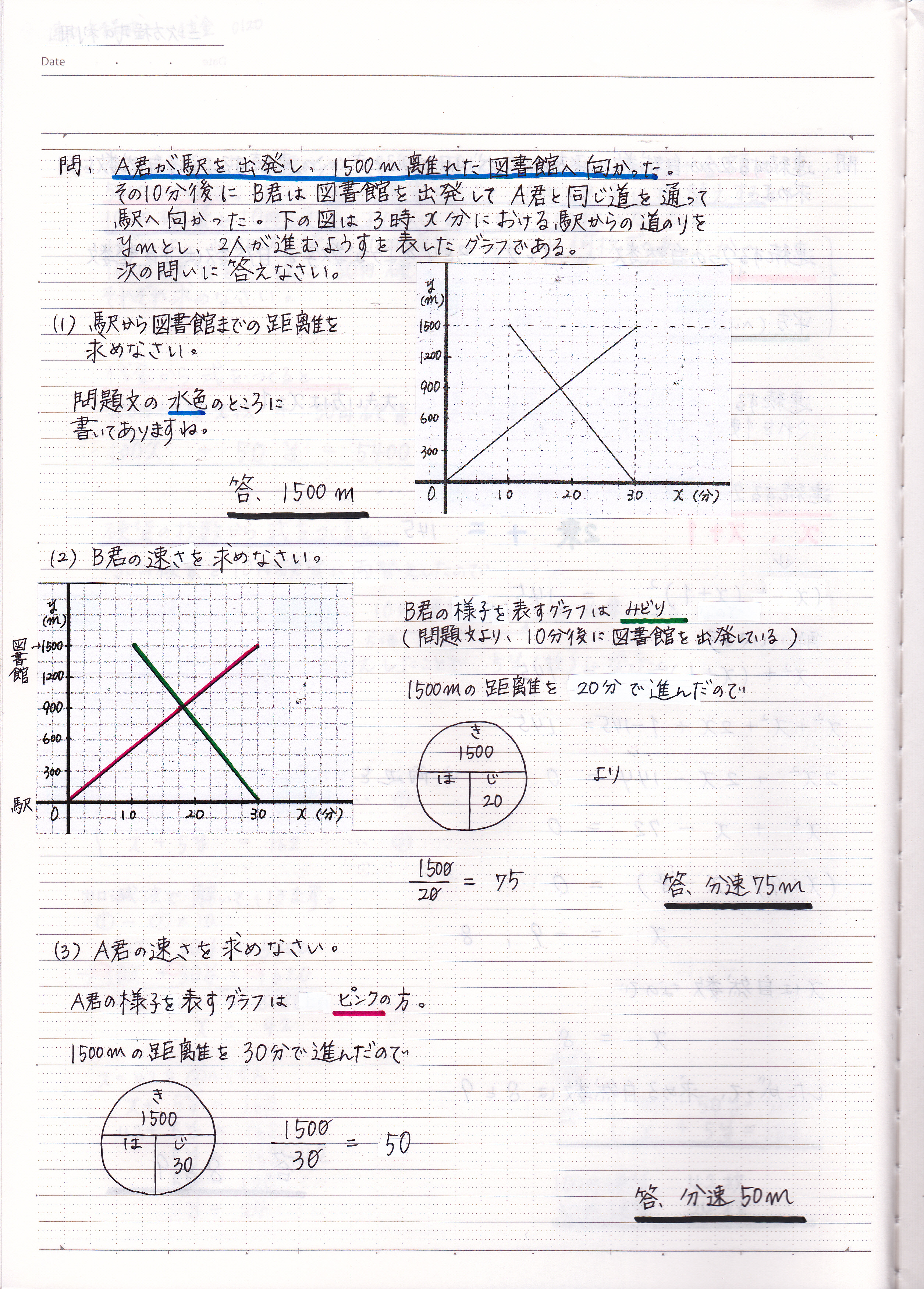



一次関数の利用の問題の解き方 速さ 3 現役塾講師のわかりやすい中学数学の解き方




2次関数の変化の割合の問題の解き方 ポイントを解説 数学fun




受験 定期試験 数学解き方集 裏技 解法 2次関数 高校
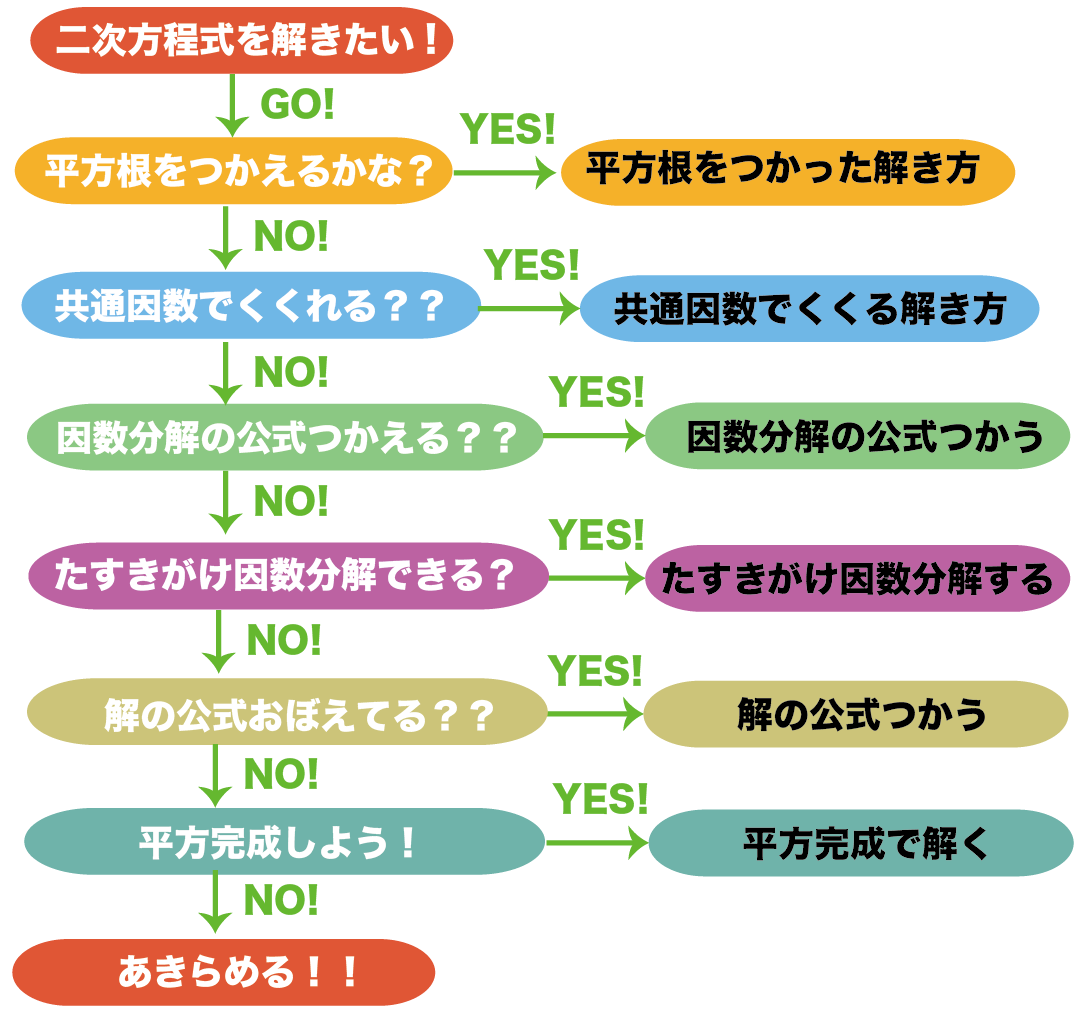



中3数学 二次方程式の解き方を見分ける1つのコツ Qikeru 学びを楽しくわかりやすく
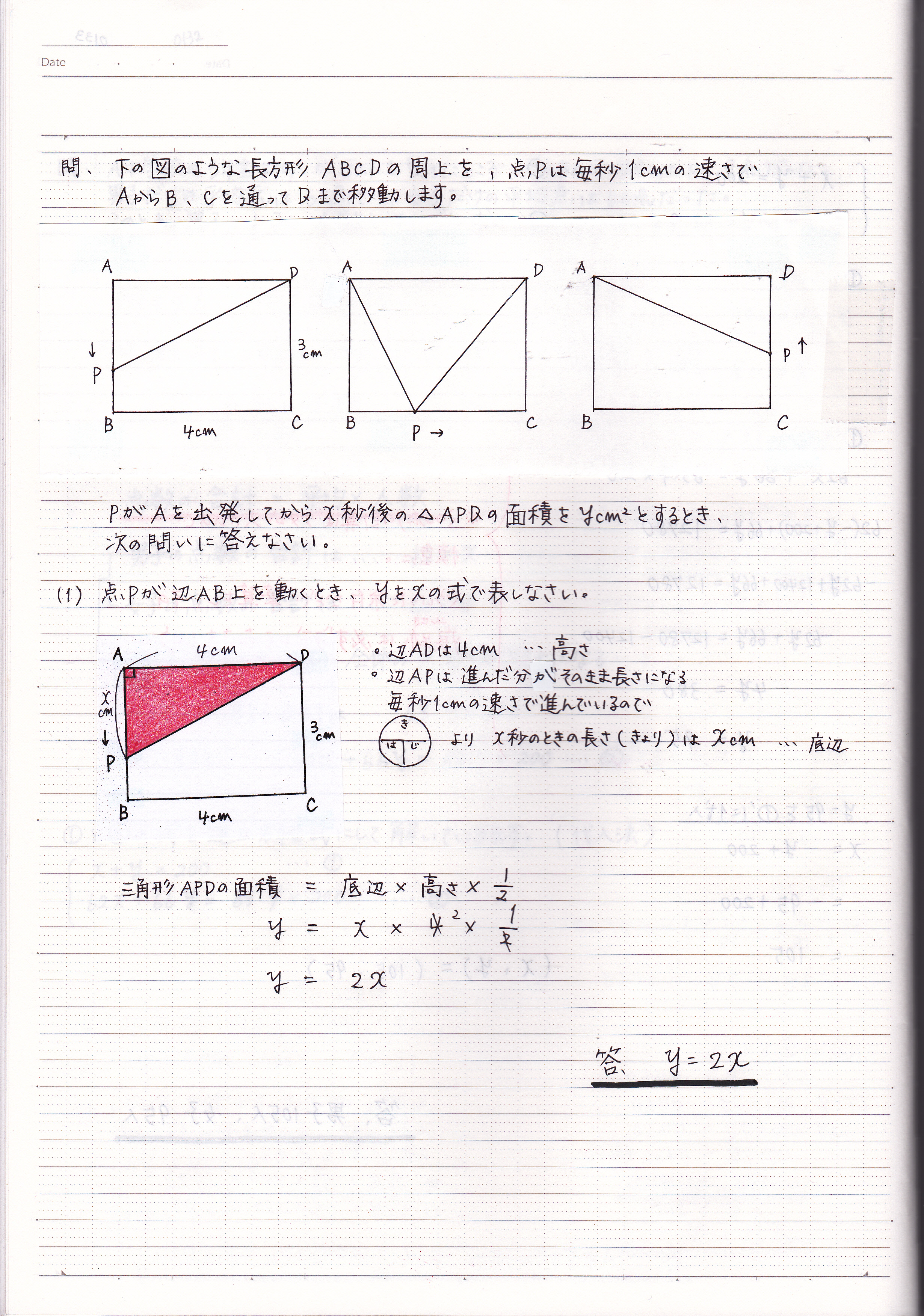



一次関数の利用の問題の解き方 動点 1 現役塾講師のわかりやすい中学数学の解き方
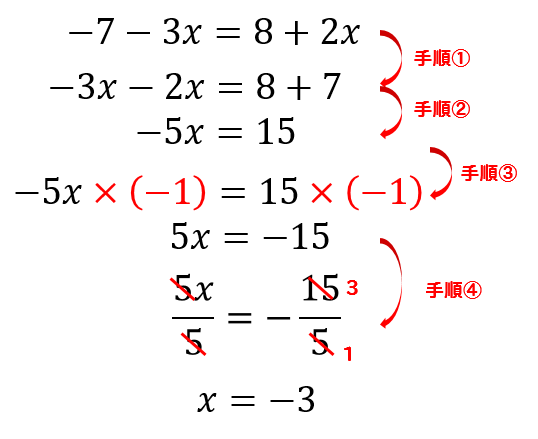



中1方程式 一次方程式の解き方をまとめておくよ 基本計算 分数 小数まで 数スタ




中2数学 一次関数の利用の問題の解き方の3つのコツ Qikeru 学びを楽しくわかりやすく




超簡単 二次不等式の解き方が誰でもわかる 必ず解きたい問題付き 高校生向け受験応援メディア 受験のミカタ
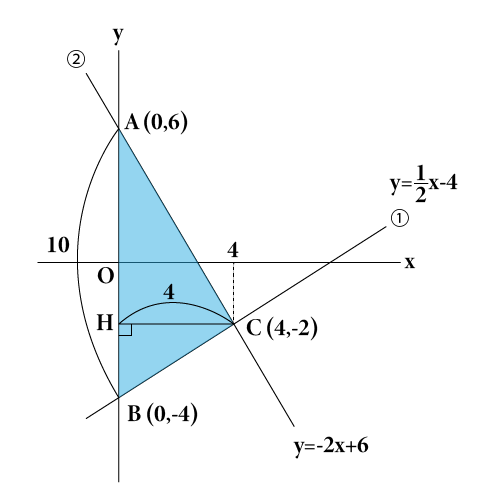



中学2年生数学 1次関数 グラフと図形 長野地区 Itto個別指導学院 長野市の学習塾




高一の対数関数です 解き方が分かりません 解説をお願いしますm M Clear




完全版 一次関数のグラフから利用問題まで解き方まとめ 中学数学 理科の学習まとめサイト




二次関数のグラフと問題の解き方 覚えておくべき2つの公式




天才数学者が考案した二次方程式 因数分解の新しい解き方 これは簡単で面白い 数学の面白いこと 役に立つことをまとめたサイト
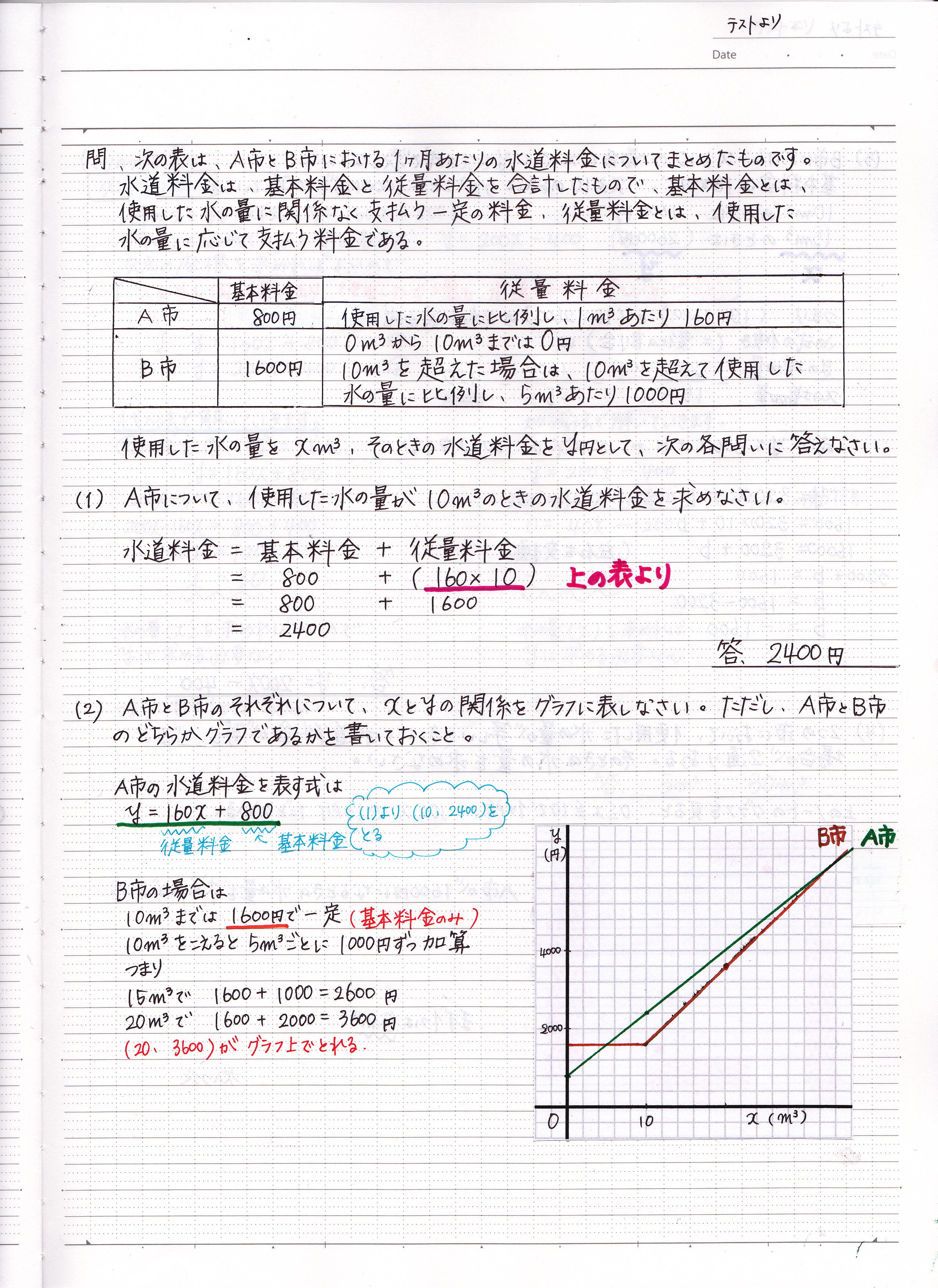



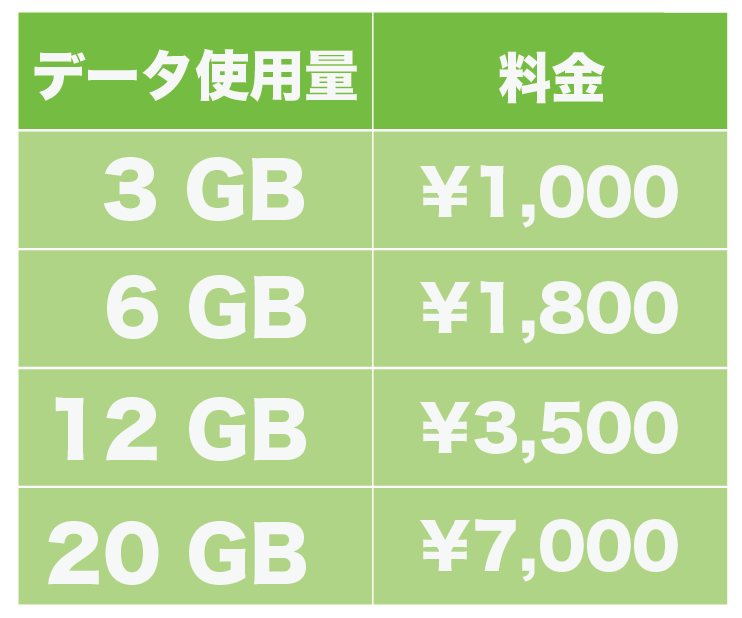
一次関数の利用の問題の解き方 料金 1 現役塾講師のわかりやすい中学数学の解き方



0 件のコメント:
コメントを投稿