2
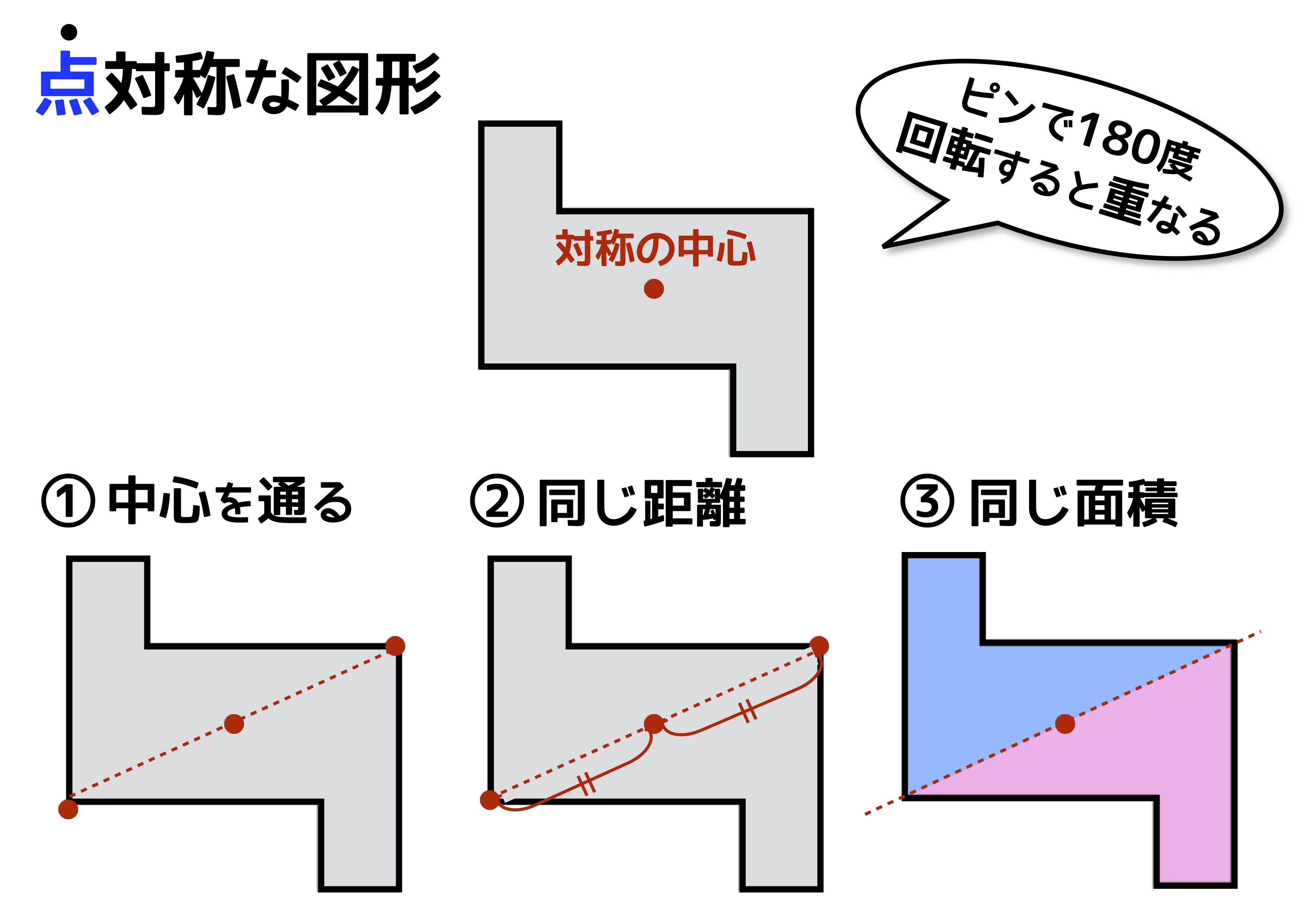
この記事では中学受験算数で出てくる「 図形の性質 」の問題について、ていねいに解説しています。今回の問題で大切になってくるのは「 線対称 」と「 点対称 」の言葉の意味を理解して作図することです。小学生の受験生にも分かるようにたくさんのイラストを使って解説しています線対称と点対称 対称(たいしょう)は、「互いに対応してつりあっていること」を意味しますが、\数学では、\(1\) 点 \(o\) を通る直線上で、\(o\) についてそれぞれ反対の側にあって、 \(o\) から等しい距離にある \(2\) 点を、\(o\) について互いに対称であると定義しています。
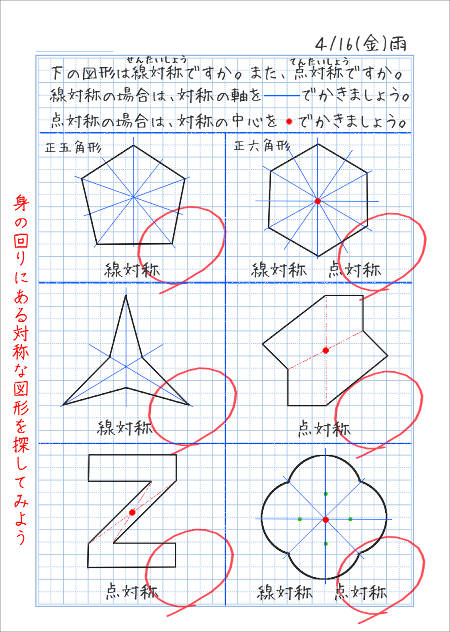
線対称 点対称 問題
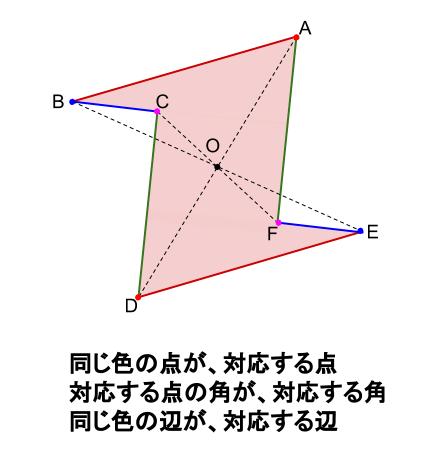
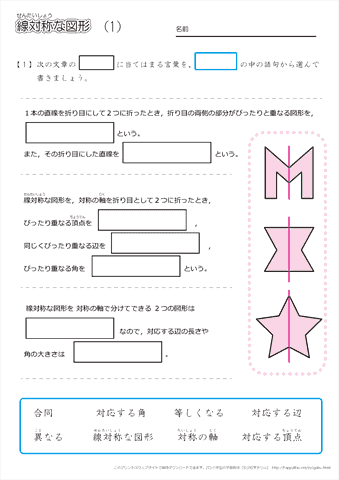
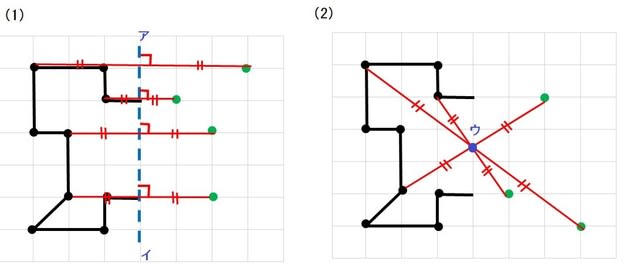
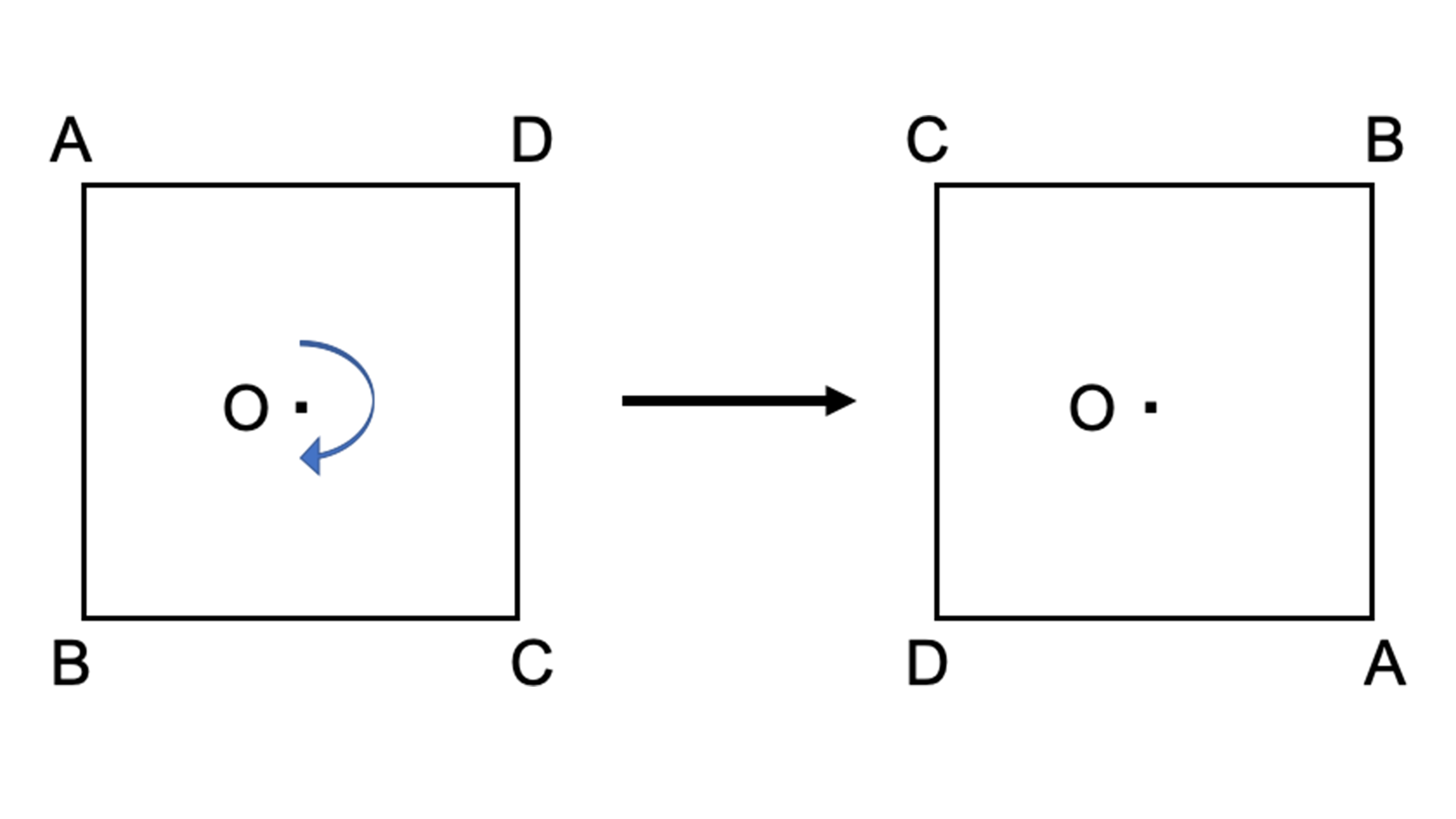
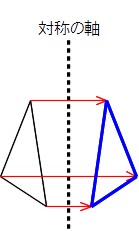
線対称 点対称 問題- ao=bo ←(点対称の性質2) 線対称の性質 ac⊥アイ ←(線対称の性質1) ao=co ←(線対称の性質2) そして線対称と点対称の図形を見分ける問題はテストなどでよく聞かれます。下の手順で見分けてみましょう。 ①図形に縦線を入れる ↓対称な図形 まとめの問題 右の図は,線対称な図形です。 ① 対称の軸をかきましょう。 ② 直線DE と対称の軸はどのように交わりますか。( ) ③ 角A と対応する角はどれですか。 ( ) ④ 辺FG の長さは何cm ですか。 ( ) 右の図は,点対称な図形です。

対称な図形 Ict教材eboard イーボード
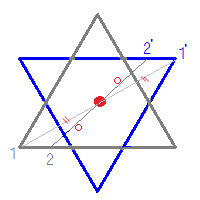
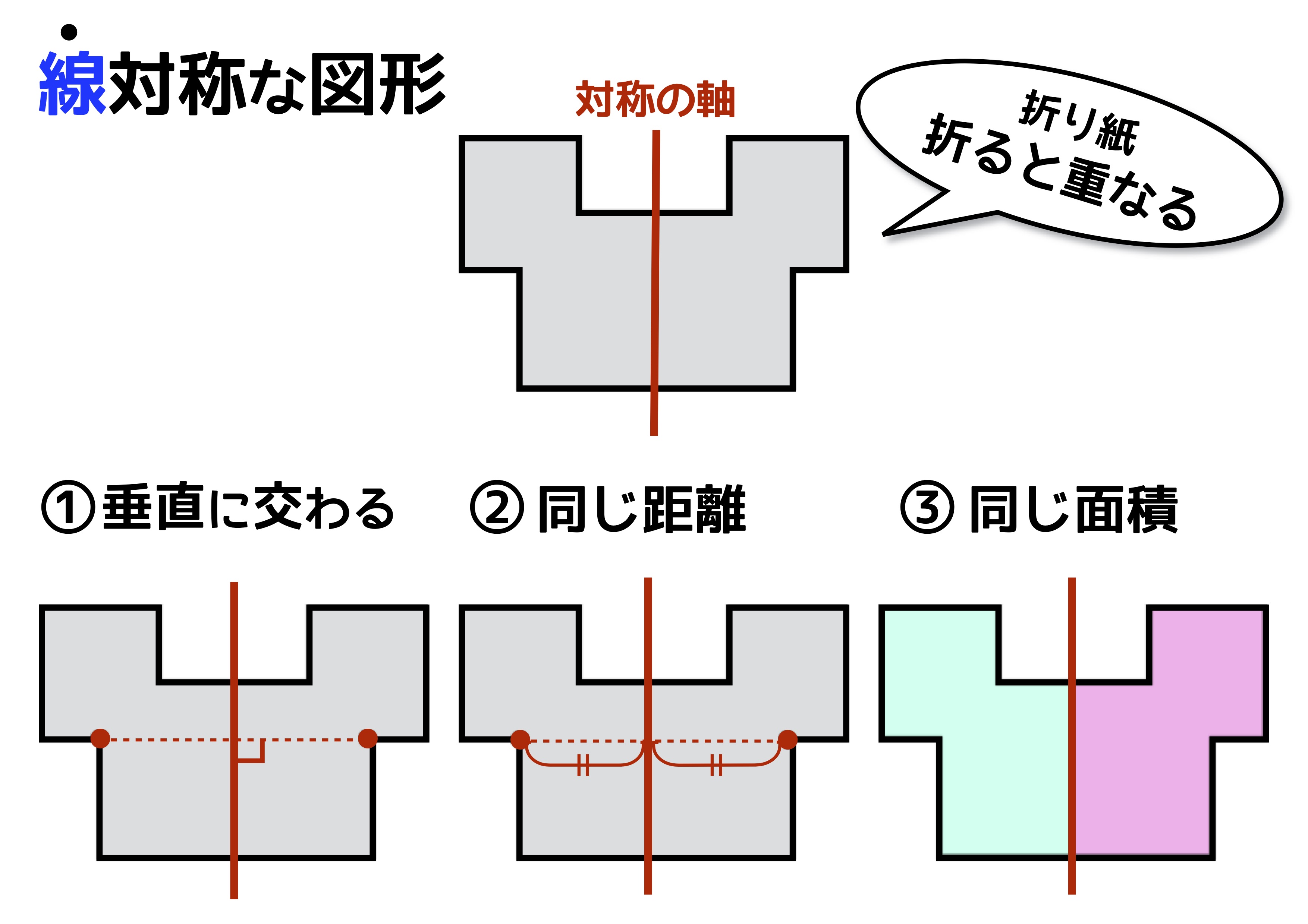
「教科書とかを見てまとめてみました( *´꒳`* ) 練習問題のページの答えのところは暗記シールを貼ってあります!」, キーワード 対称な図形,線対称,点対称,あおりんご 差をつける自宅学習を始めよう すべての3次関数のグラフは変曲点に関して点対称であることが知られています。 変曲点については,数学IIIを学習している人にとっては常識かもしれませんが,そうでない人にとっては知らないことかもそして「対応する点を結ぶと対称の軸と 垂直 になり、それぞれの点から軸までの距離が 等距離 になる」という性質があります。 ちなみに線対称は対称の軸が複数存在することがあり、正五角形の場合5本の対称の軸が存在します。
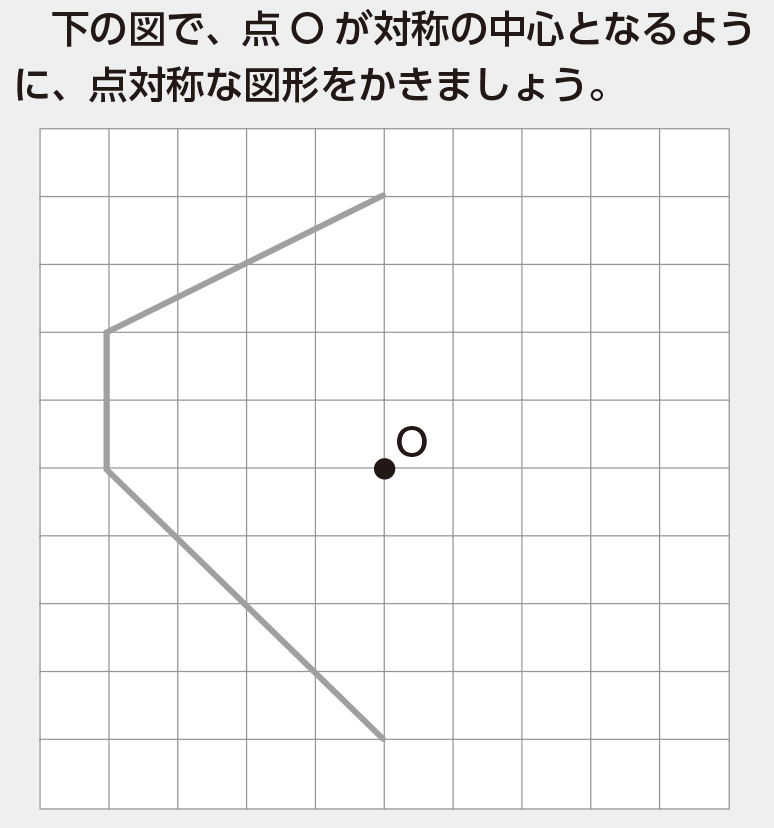
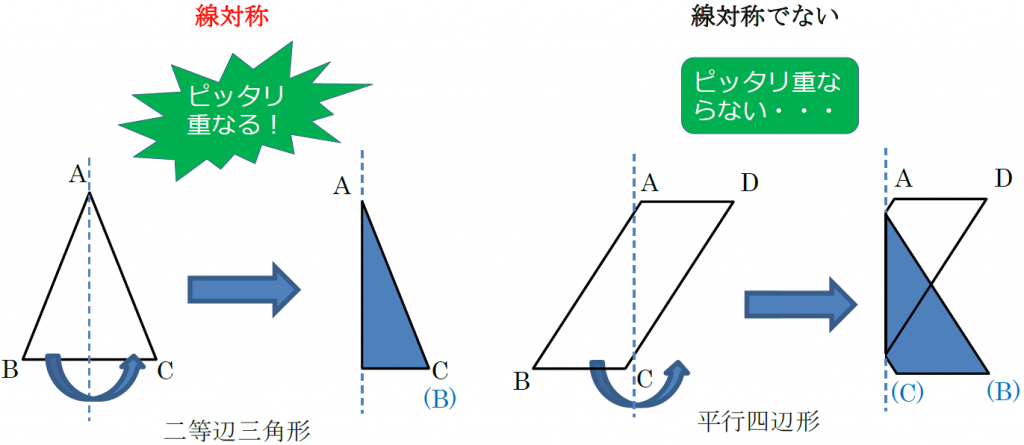
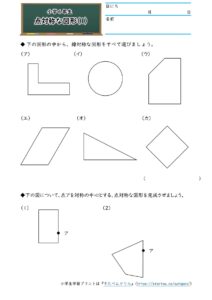
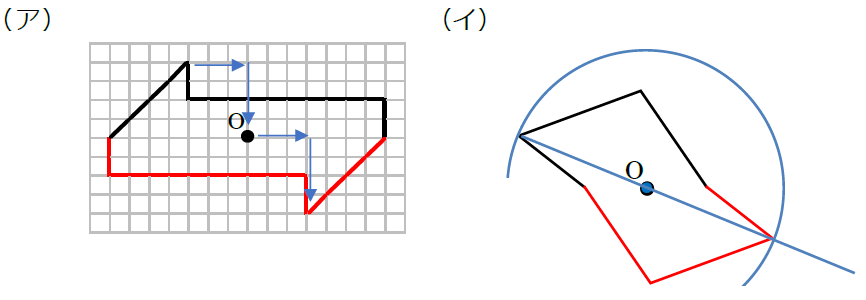
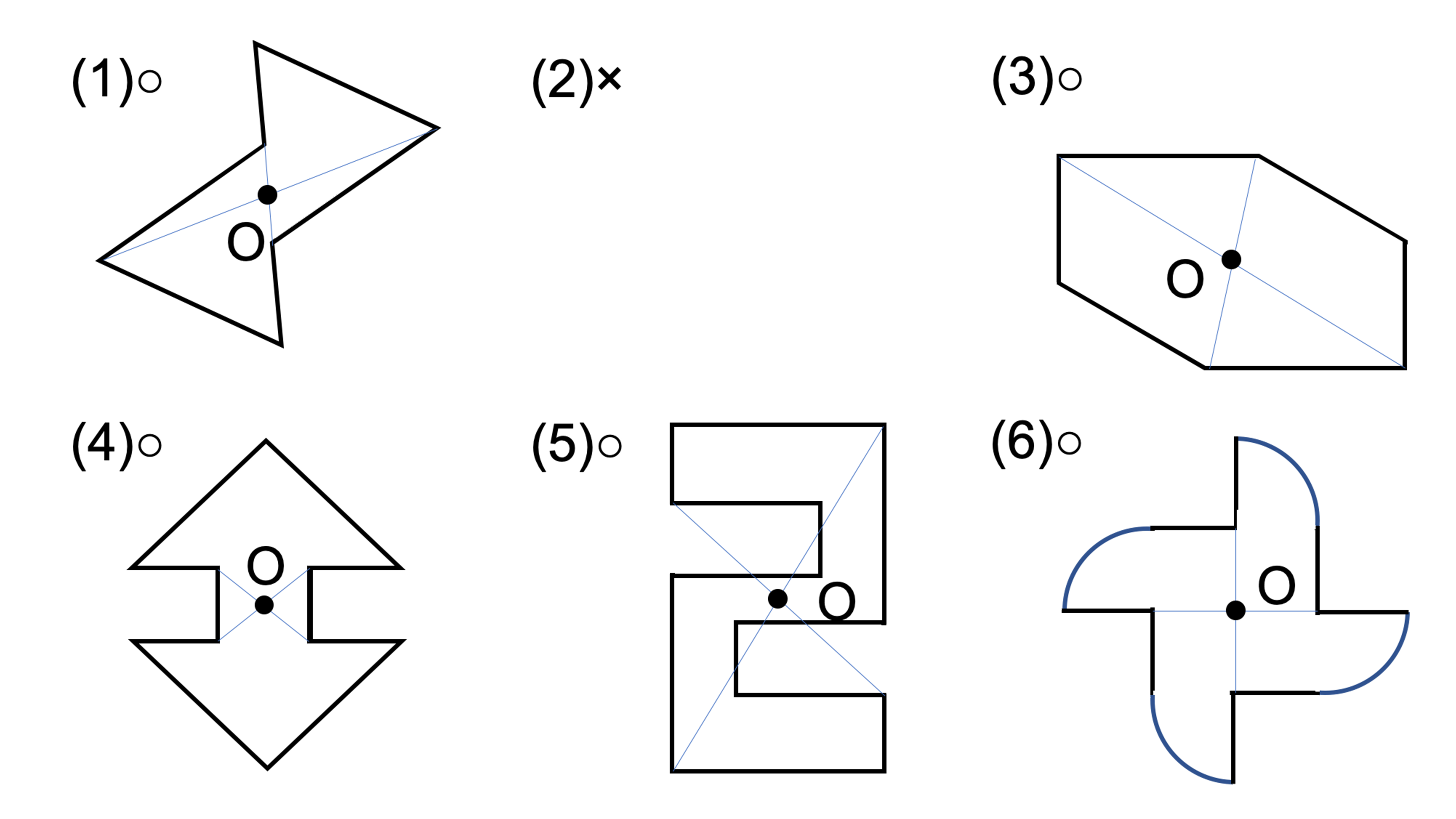
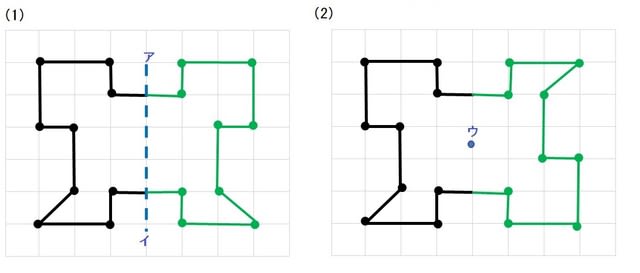
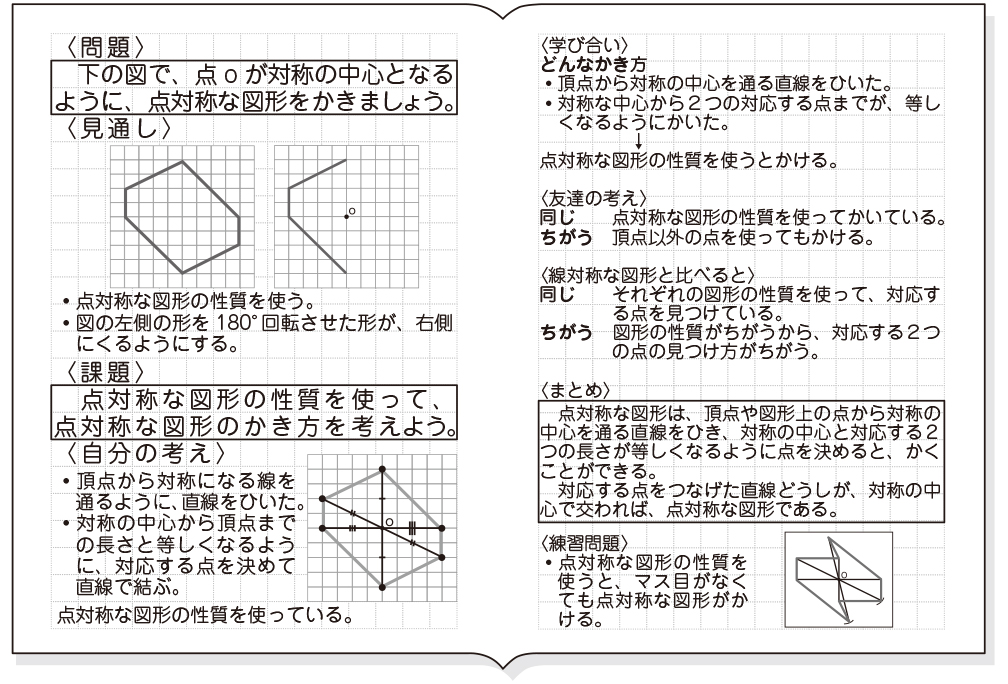
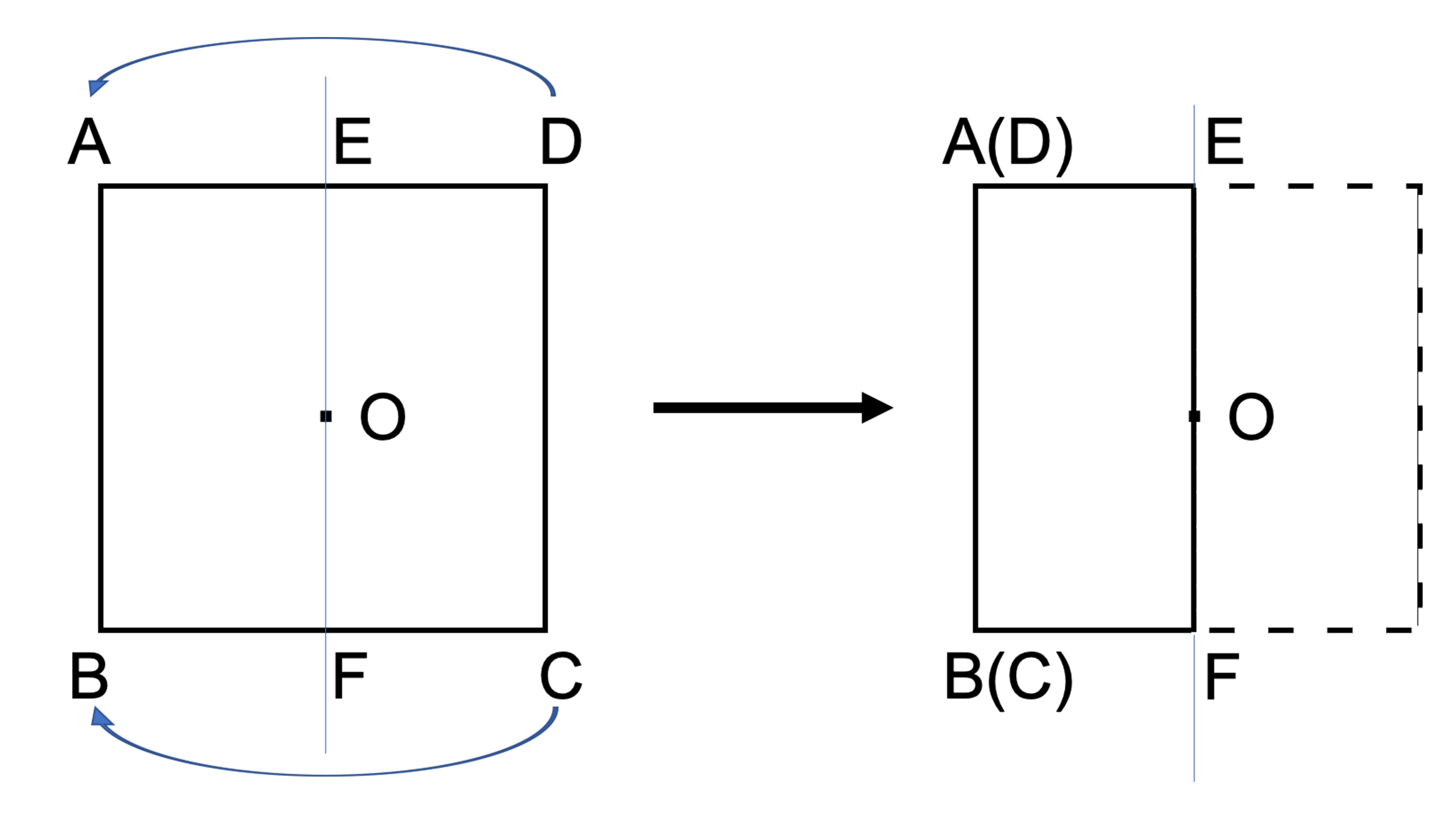
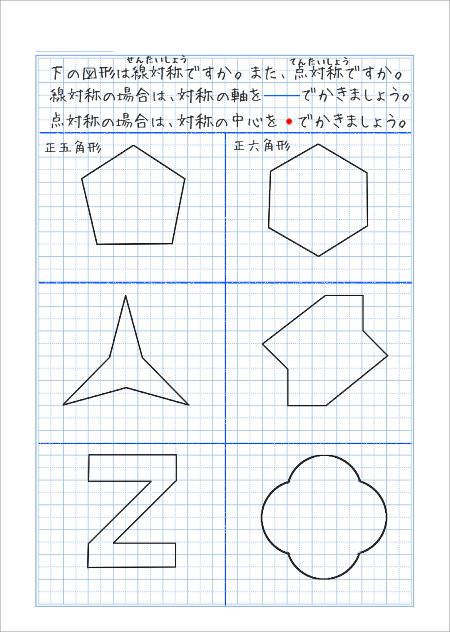
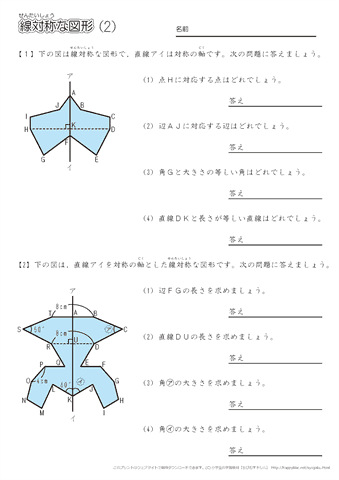
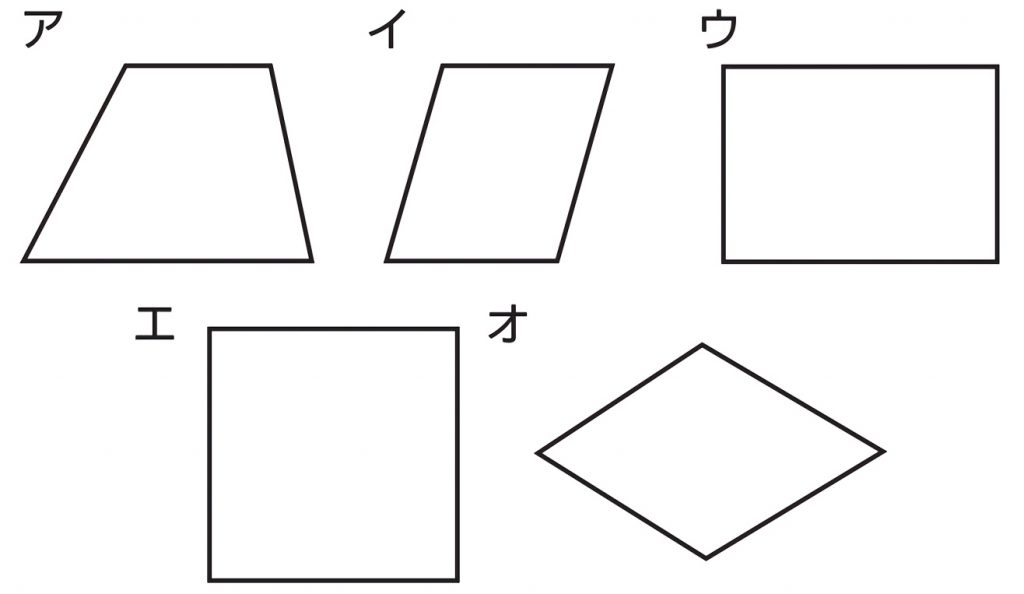
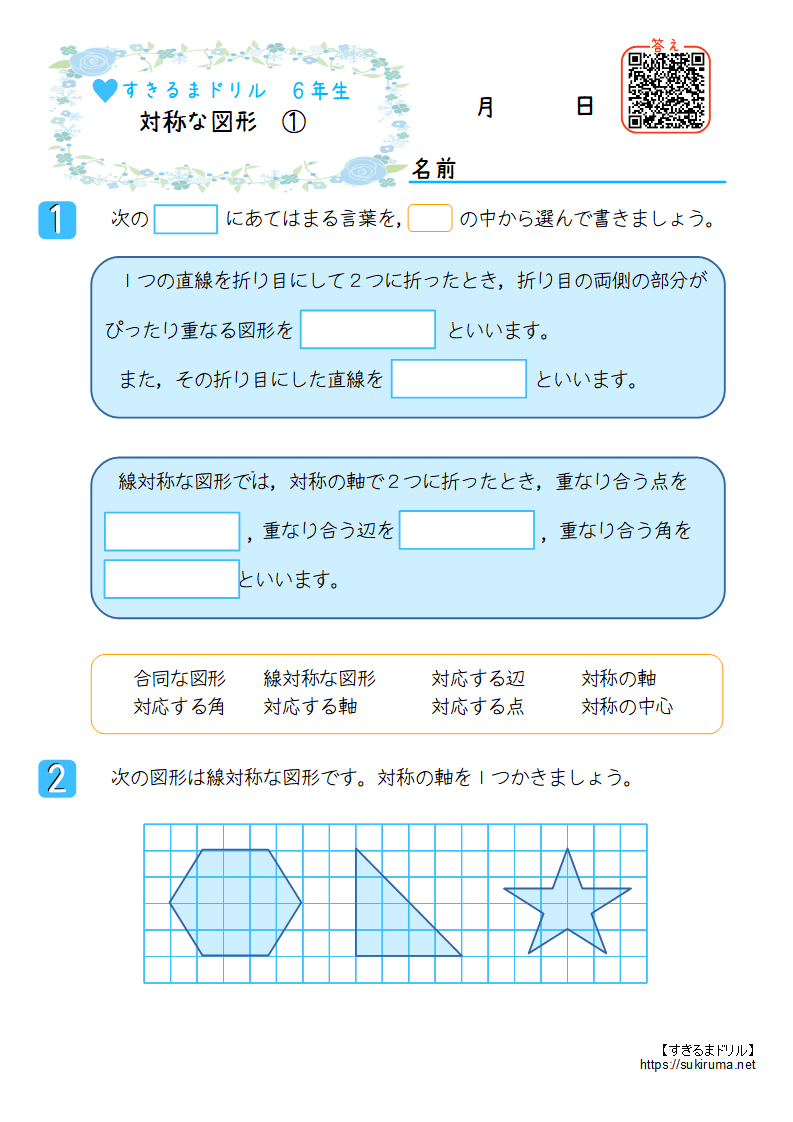
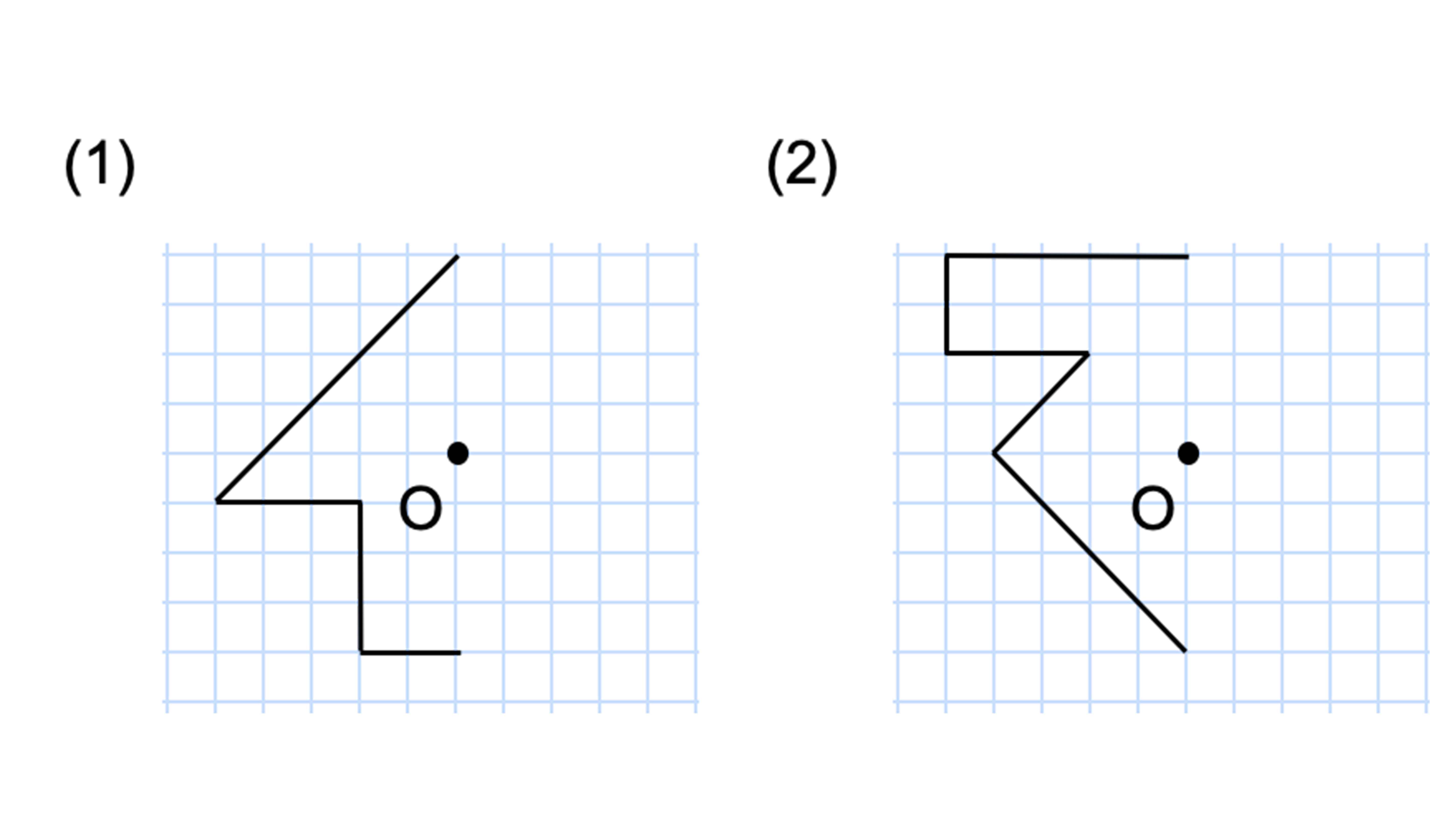
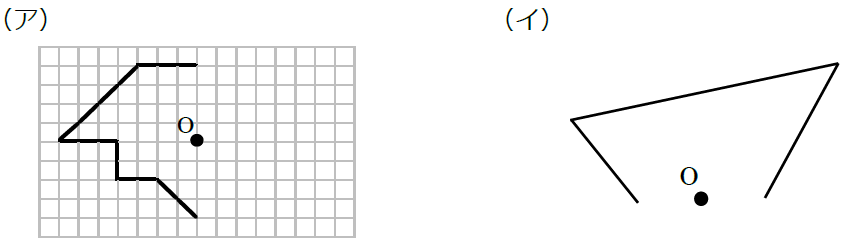
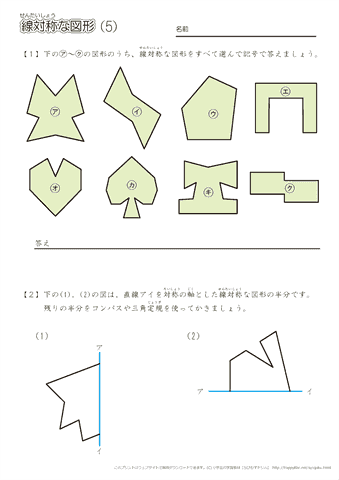
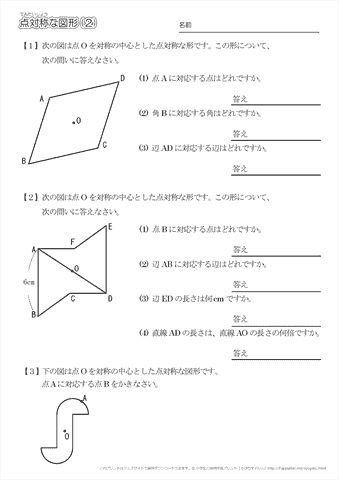
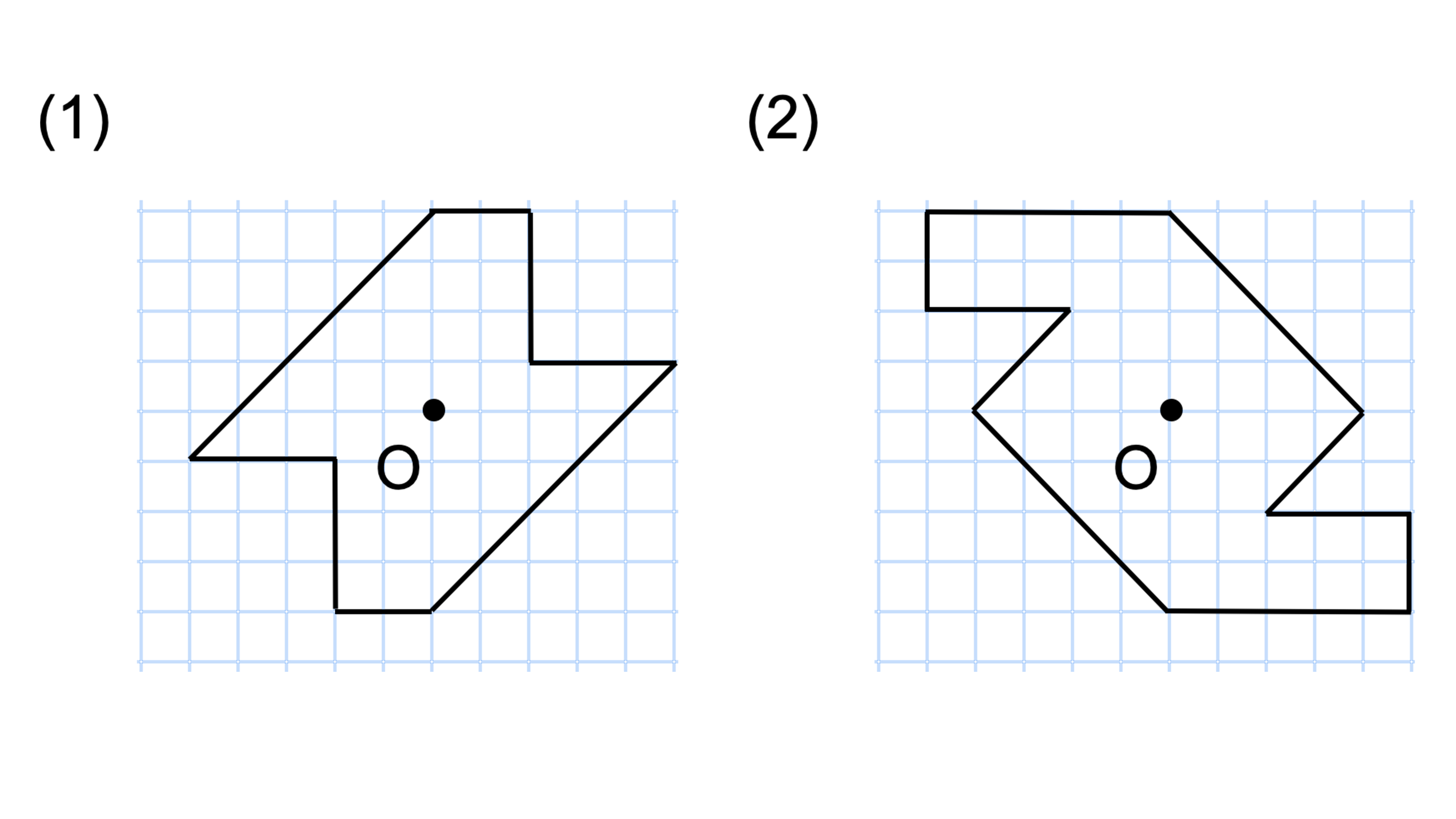
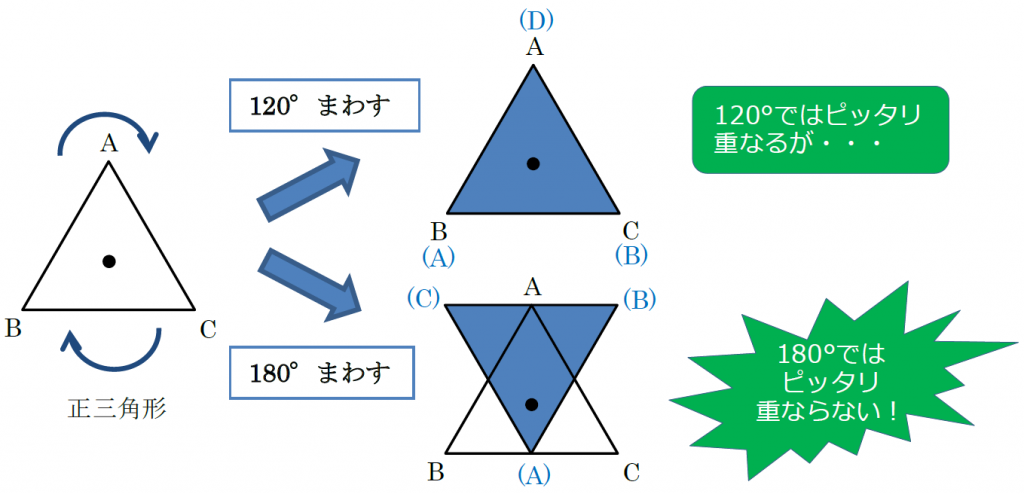
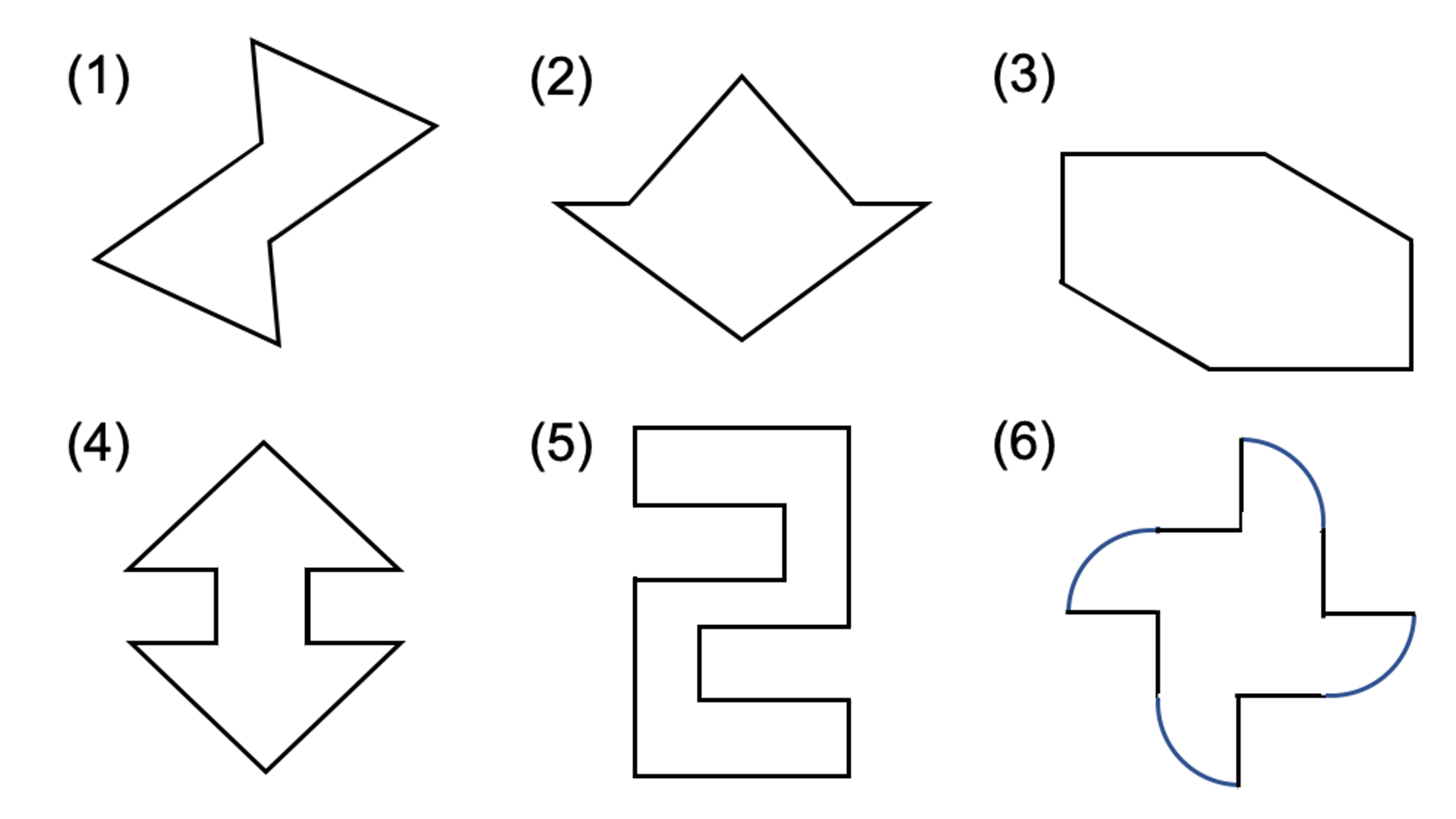
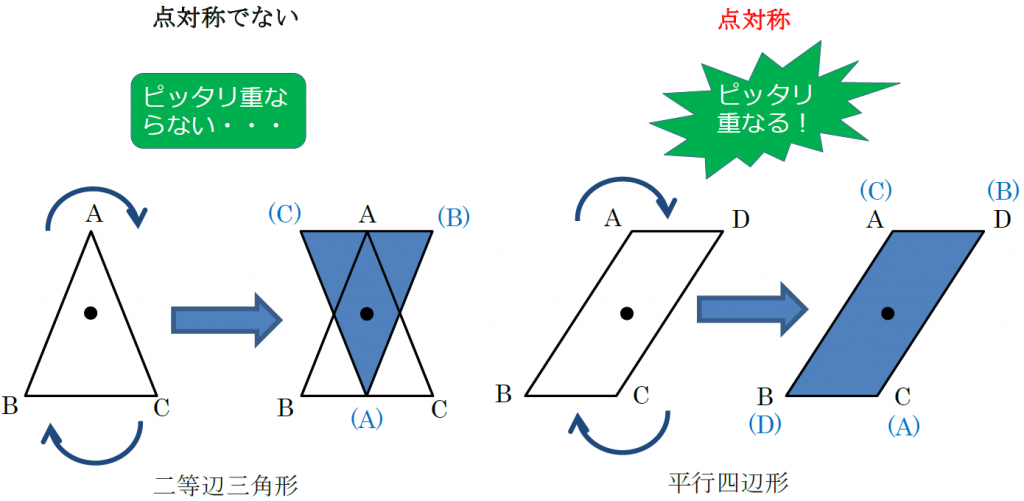
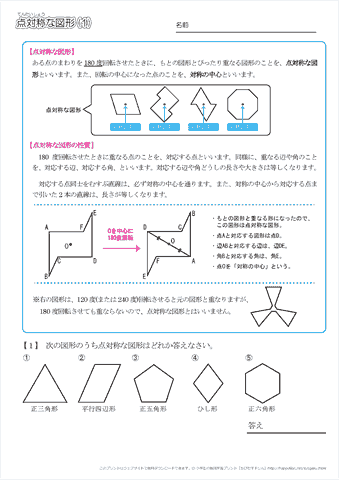
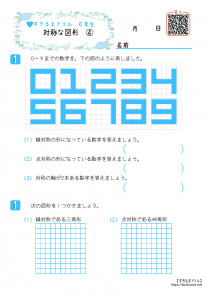
この問題は与えられた図形が 「線対称である」 のか、 「点対称である」 のか、「 線対称であり、点対称である」 のか、 「どちらでもない」 のかの、4つの選択肢から1つの解答を導く問題と言えます。線対称と点対称の定義は次のように与えられています。@ Ⴆ C p ` ̓_1 璆 S ܂ł̋ " 𒆐S ̔ Α ɐL _1' ͌ ̐ p ` ̏ ɂ C _2 璆 S ܂ł̋ o 𒆐S ̔ Α ɐL _2' ̐ p ` ̏ ɂ D @ ̂悤 ɁC ̐ p ` i D F j 180 ƌ ̐} ` ƈ v D y T z @ p ` ͓_ Ώ̂Ȑ} ` ł͂Ȃ D1 次の図形から,点対称な図形と線対称な図形を答えましょう。 線対称な図形 点対称な図形 2 下の図は線対称な図形です。 ⑴ 対称の軸は,どれですか。 ⑵ 点Fに対応する点は,どれですか。 ⑶ 直線BCに対応する直線は,どれですか。
線対称 点対称 問題のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 | ||
「線対称 点対称 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  | |
「線対称 点対称 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「線対称 点対称 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「線対称 点対称 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「線対称 点対称 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「線対称 点対称 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「線対称 点対称 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「線対称 点対称 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「線対称 点対称 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 | ||
「線対称 点対称 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「線対称 点対称 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |
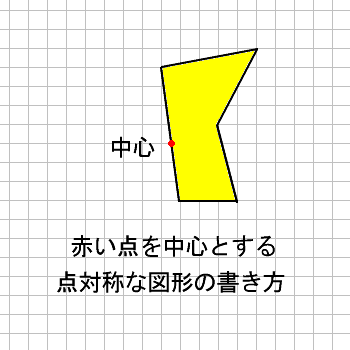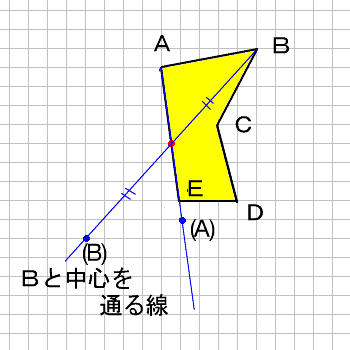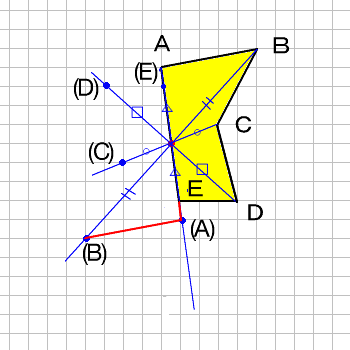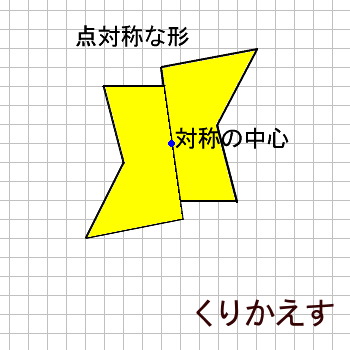
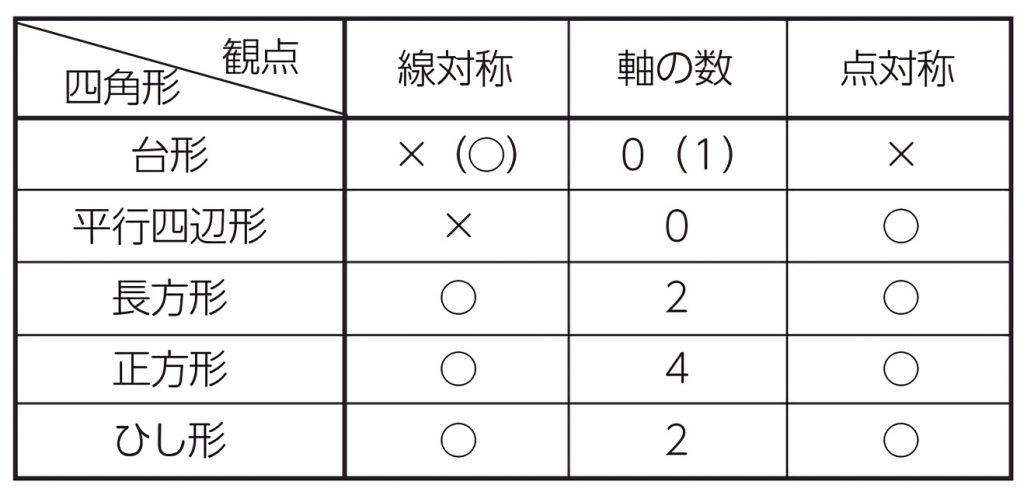
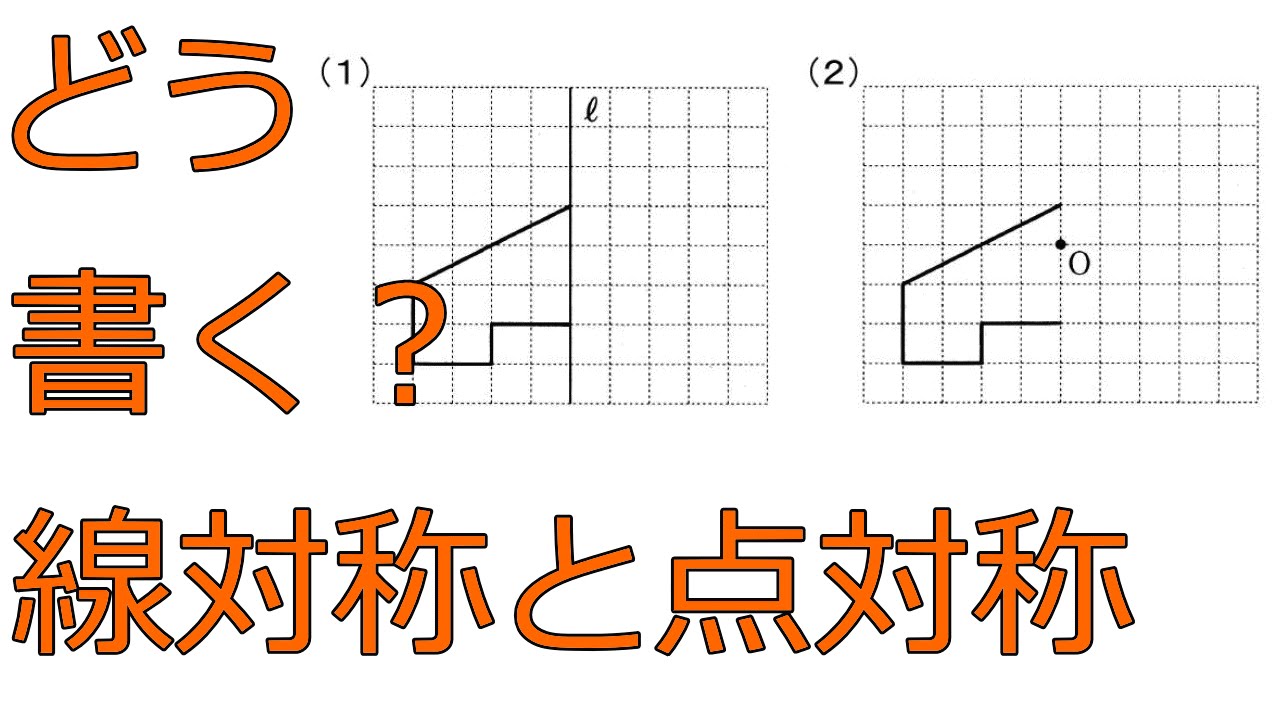
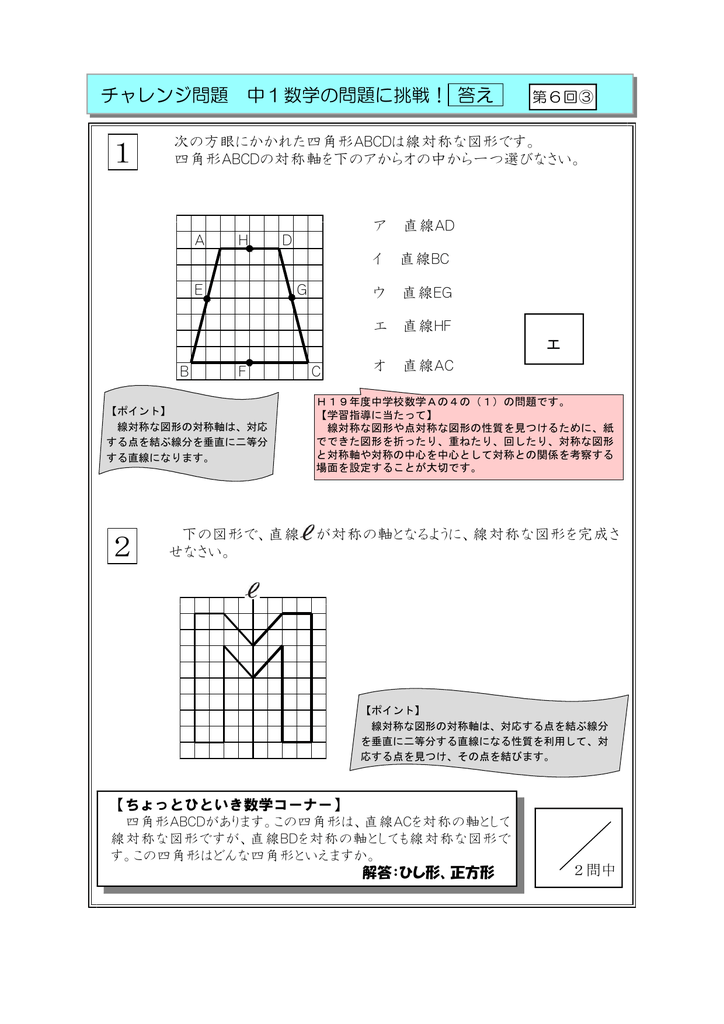
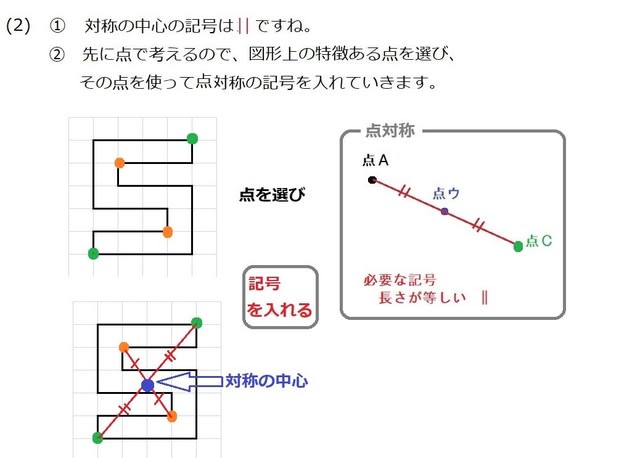
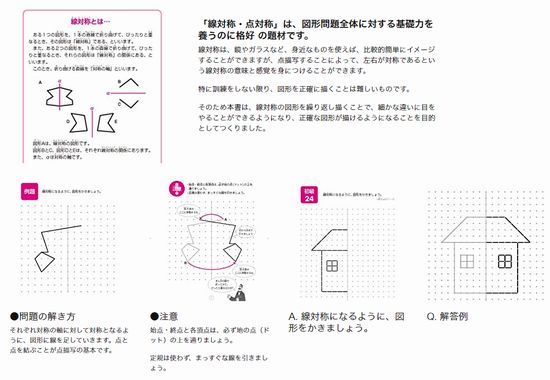
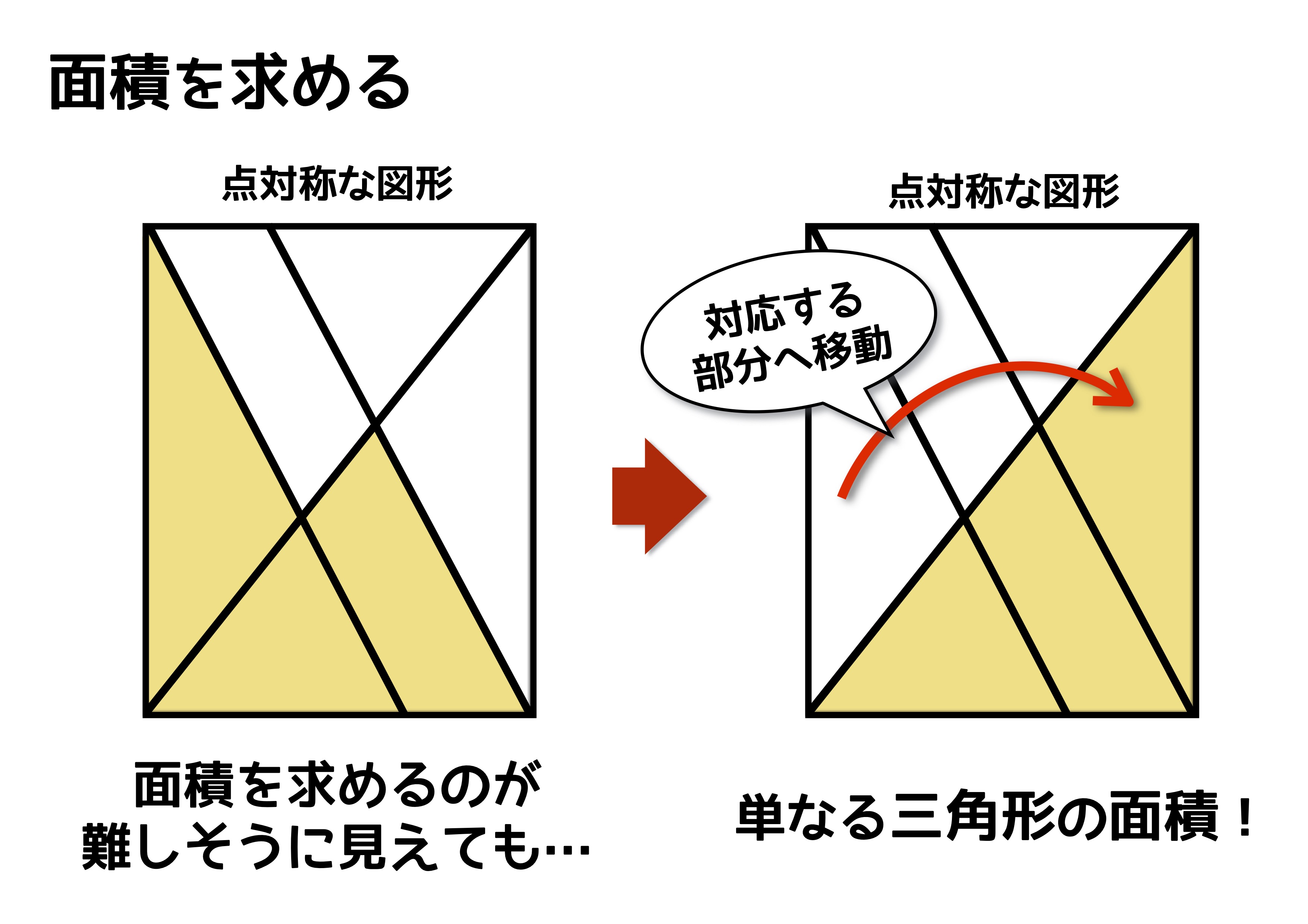
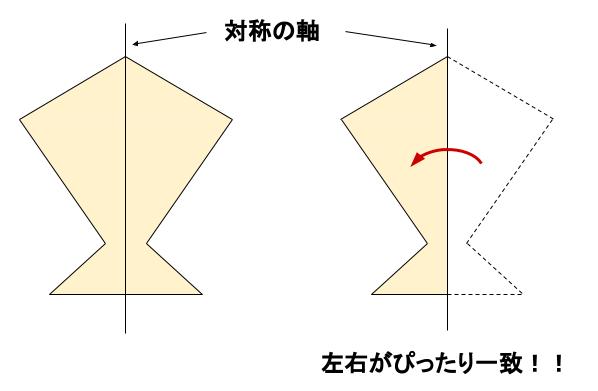
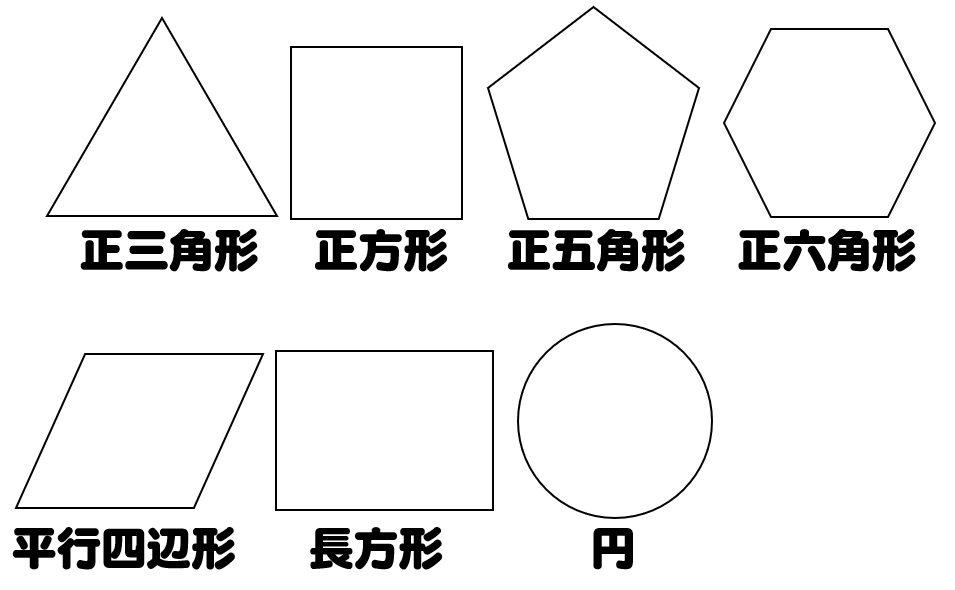
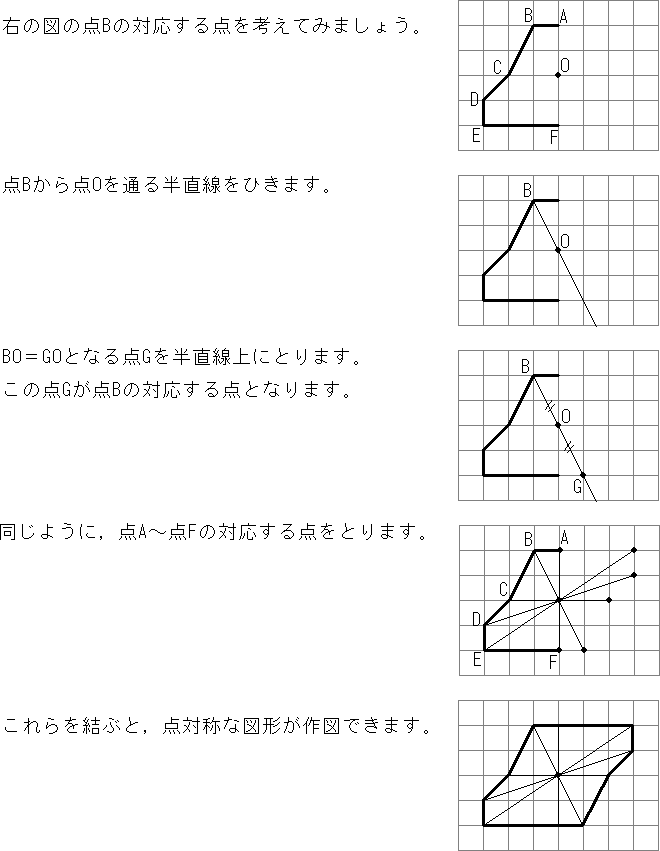
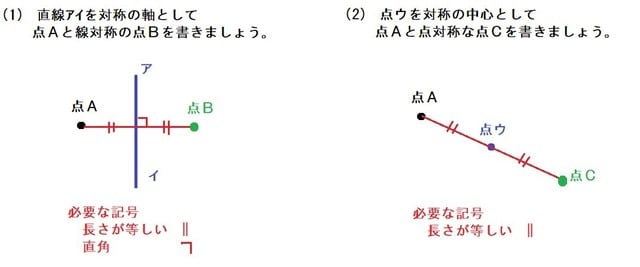
だから点対称の場合は中点を利用して求めよう。それが簡単だからね。 あと、点対称を求める場合は どの点に関して対称なのか 問題文をよく読もう。 「点\(\small{ \ \mathrm{A} \ }\)に関して対称」って言われたら点\(\small{ \ \mathrm{A} \ }\)が中点になるってことだからね。線対称,点対称 線対称な図形 解説 ある直線を折り目として折り返したとき,両側の図形がピッタリと重なる図形を 線対称 な図形といい,このときの直線を 対称軸 といいます。 次の例1では,対称軸が1本あります。 例1 次の例2 (正方形)では対称軸が4
Incoming Term: 線対称 点対称 問題, 線対称 点対称 問題 難しい,




0 件のコメント:
コメントを投稿